题目内容
已知AB与CD相交于点O,OA=12,OB=6,OC=8,且
=
,求CD的长.
| AB |
| AO |
| CD |
| CO |
考点:平行线分线段成比例
专题:
分析:先由OA=12,OB=6,得出AB=OA+OB=18,再根据
=
,得出
=
,即可求出CD=12.
| AB |
| AO |
| CD |
| CO |
| 18 |
| 12 |
| CD |
| 8 |
解答: 解:如图,∵OA=12,OB=6,
解:如图,∵OA=12,OB=6,
∴AB=OA+OB=18,
又∵OC=8,
=
,
∴
=
,
∴CD=12.
 解:如图,∵OA=12,OB=6,
解:如图,∵OA=12,OB=6,∴AB=OA+OB=18,
又∵OC=8,
| AB |
| AO |
| CD |
| CO |
∴
| 18 |
| 12 |
| CD |
| 8 |
∴CD=12.
点评:本题考查了比例的性质,利用数形结合是解题的关键.

练习册系列答案
相关题目
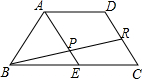 在等腰梯形ABCD中,下底BC是上底AD的两倍,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP=( )
在等腰梯形ABCD中,下底BC是上底AD的两倍,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP=( )A、
| ||
B、
| ||
C、
| ||
D、
|
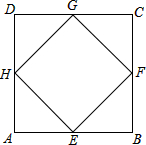 (1)如图,顺次连接正方形ABCD的各边中点,得到一个小正方形EFGH.则正方形EFGH与正方形ABCD的面积比是多少?
(1)如图,顺次连接正方形ABCD的各边中点,得到一个小正方形EFGH.则正方形EFGH与正方形ABCD的面积比是多少?