题目内容
8.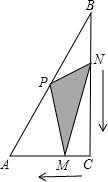 如图,在△ABC中,∠C=90°,点P是斜边AB的中点,点M从点C向点A匀速运动,点N从点B向点C匀速运动,已知两点同时出发,同时到达终点,连接PM、PN、MN,在整个运动过程中,△PMN的面积S与运动时间t的函数关系图象大致是( )
如图,在△ABC中,∠C=90°,点P是斜边AB的中点,点M从点C向点A匀速运动,点N从点B向点C匀速运动,已知两点同时出发,同时到达终点,连接PM、PN、MN,在整个运动过程中,△PMN的面积S与运动时间t的函数关系图象大致是( )| A. | 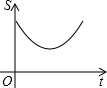 | B. |  | C. |  | D. | 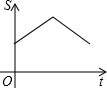 |
分析 首先连接CP,根据点P是斜边AB的中点,可得S△ACP=S△BCP=$\frac{1}{2}$S△ABC;然后分别求出出发时;点N到达BC的中点、点M也到达AC的中点时;结束时,△PMN的面积S的大小,即可推得△MPN的面积大小变化情况是:先减小后增大,而且是以抛物线的方式变化,据此判断出△PMN的面积S与运动时间t的函数关系图象大致是哪个即可.
解答 解:如图1,连接CP,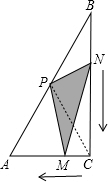 ,
,
∵点P是斜边AB的中点,
∴S△ACP=S△BCP=$\frac{1}{2}$S△ABC,
出发时,S△PMN=S△BCP=$\frac{1}{2}$S△ABC;
∵两点同时出发,同时到达终点,
∴点N到达BC的中点时,点M也到达AC的中点,
∴S△PMN=$\frac{1}{4}$S△ABC;
结束时,S△PMN=S△ACP=$\frac{1}{2}$S△ABC,
在整个运动过程中设BC=a,AC=b,
∴S=$\frac{1}{2}$[ab-VN•t•$\frac{b}{2}$-(a-VN•t)•VM•t-(b-VM•t)•$\frac{a}{2}$]
=$\frac{1}{2}$(ab-$\frac{1}{2}$VNb•t-aVM•t+VNVM•t2-$\frac{1}{2}$ab+$\frac{1}{2}$aVM•t)
=$\frac{1}{2}$VNVM•t2-$\frac{1}{4}$(VNb+aVM)t+$\frac{1}{4}$ab,
∴△MPN的面积大小变化情况是:先减小后增大,而且是以抛物线的方式变化,
∴△PMN的面积S与运动时间t的函数关系图象大致是: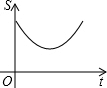 .
.
故选:A.
点评 此题主要考查了动点问题的函数图象,要熟练掌握,解答此题的关键是要明确:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.用图象解决问题时,要理清图象的含义即会识图.

 如图,在四边形ABCD中,下列条件中可以判定AD∥BC的是( )
如图,在四边形ABCD中,下列条件中可以判定AD∥BC的是( )| A. | ∠1=∠3 | B. | ∠2=∠4 | C. | ∠B=∠D | D. | ∠B+∠BCD=180° |
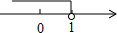 不等式ax-2<0的解集在数轴上表示如图,那么a的取值范围是( )
不等式ax-2<0的解集在数轴上表示如图,那么a的取值范围是( )| A. | a<1 | B. | a<2 | C. | a=1 | D. | a=2 |
 如图,过Rt△ABC的直角顶点C作直线CD∥AB,则图中与∠CAB互余的角共有( )
如图,过Rt△ABC的直角顶点C作直线CD∥AB,则图中与∠CAB互余的角共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
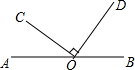 如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )| A. | 34° | B. | 44° | C. | 54° | D. | 64° |
| A. | x2•x3=x6 | B. | 5x-2x=3x | C. | (x2)3=x5 | D. | (-2x)2=-4x2 |