Question

5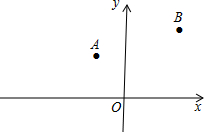．如图，在平面直角坐标系中，点A（-2，3），B（4，5），点P是x轴上一动点．求：
①PA+PB的最小值及此时点P的坐标；
②|PA-PB|的最大值及此时点P的坐标．

Answer 1

分析 （1）先画出图形，由两点之间线段最短可知，当P点在线段AB上时PA+PB的值最小，即PA+PB=AB，利用两点间的距离公式求解即可，然后过点B作BD⊥x轴垂足为D，接下来证明△CPA′∽△DPB，由相似三角形的性质可求得PC的长，从而可得到点P的坐标；
（2）作直线AB与x轴交与点P，作AC⊥x轴，BD⊥x轴．PA-PB|的最大值=AB，然后证明△PAC∽△PBD，从而可求得PC的长，故此可求得点P的坐标．

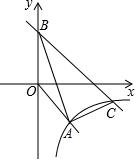
解答 解：（1）如图1所示：作点A关于x轴的对称点A′，连结A′B交x轴与点P．

∵点A′关于点A对称，
∴点A′的坐标为（-2，-3）．
∴AP+BP=A′P+PB=A′B=10．
∴PA+PB的最小值为10．
过点B作BD⊥x轴垂足为D．
∵△CPA′∽△DPB，
∴CP：DP=CA′：BD=3：5．
又∵CD=6，
∴CP=6×$\frac{3}{8}$=$\frac{9}{4}$．
∴OP=$\frac{1}{4}$．
∴点P的坐标为（$\frac{1}{4}$，0）．
（2）如图2所示，作直线AB与x轴交与点P，作AC⊥x轴，BD⊥x轴．

当点P在直线AB上时，|PA-PB|的最大值=AB=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$．
∵AC∥BD，
∴△PAC∽△PBD．
∴$\frac{PC}{PD}=\frac{PA}{PB}$即$\frac{PC}{PC+6}=\frac{3}{5}$．
解得PC=9．
∴PO=9+2=11．
∴点P的坐标为（-11，0）．

点评 本题考查的是线路最短问题，解答此题的关键是画出图形，利用数形结合及两点间的距离公式求解．