Question

12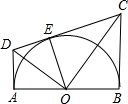．如图，AB为半圆O的直径，AD、BC分别切⊙O于A，B两点，CD切⊙O于点E，AD与CD相交于D，BC与CD相交于C，连结OD、OE、OC，对于下列结论：
①AD+BC=CD；②∠DOC=90°；③S_梯形ABCD=$\frac{1}{2}$CD•OA；④$\frac{OD}{DE}=\frac{CD}{OD}$．
其中结论正确的个数是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 利用切线长定理得到AD=ED，CE=CB，且OD、OC分别为角平分线，利用平角的定义及等式性质得到∠COD为直角，进而确定出三角形ODE与三角形COD相似，由相似得比例列出关系式，根据CD=DE+EC，等量代换得到AD+BC=CD，即可得到正确的选项．

解答 解：∵DA、DE为圆O的切线，
∴AD=ED，∠AOD=∠EOD，
∵CE、CB为圆O的切线，
∴CE=CB，∠EOC=∠BOC，
∴CD=DE+EC=AD+BC，选项①正确；
∵∠AOD+∠DOE+∠EOC+∠BOC=180°，
∴∠DOE+∠EOC=90°，即∠DOC=90°，选项②正确；
∵S_梯形ABCD=$\frac{1}{2}$（AD+BC）•AB=$\frac{1}{2}$（DE+CE）•2OA=CD•OA，
∴选项③错误；
∵OE⊥CD，
∴∠OED=∠COD=90°，
∵∠EDO=∠ODC，
∴△DOE∽△CDE，
∴$\frac{OD}{DE}=\frac{CD}{OD}$，
∴选项④正确；
故选C．

点评 此题考查了切线的性质，相似三角形的判定与性质，熟练掌握切线的性质是解本题的关键．