题目内容
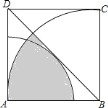
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 、
、![]() 是
是![]() 的切线,切点分别为
的切线,切点分别为![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.

![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 若
若![]() ,
,![]() ,求阴影部分的面积.(结果保留
,求阴影部分的面积.(结果保留![]() )
)
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)首先作OH⊥CD,垂足为H,由BC、AD是⊙O的切线,易证得△BOC≌△AOE(ASA),继而可得OD是CE的垂直平分线,则可判定DC=DE,即可得OD平分∠CDE,则可得OH=OA,证得CD是⊙O的切线;
(2)首先证得△AOE∽△ADO,然后由相似三角形的对应边成比例,求得OA的长,然后利用三角函数的性质,求得∠DOA的度数,继而求得答案.
(1)作![]() ,垂足为
,垂足为![]() ,
,
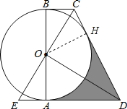
∵![]() 、
、![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
在![]() 和
和![]() 中,
中,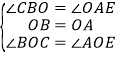 ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线;
的切线;
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目