Question

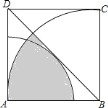
【题目】如图所示，以正方形的顶点为圆心的弧恰好与对角线相切，以顶点为圆心，正方形的边长为半径的弧，已知正方形的边长为，则图中阴影部分的面积为（ ）

A. B. C. D.

Answer 1

【答案】D

【解析】

连接AC交BD于O，由正方形的性质得出OA=OB=BD，AC⊥BD，∠BAD=90°，AB=AD=2，∠BAO=∠ABF=45°，由勾股定理求出BD，得出OA=OB=，求出△AOB的面积、扇形AOE的面积、扇形ABF的面积，即可得出图中阴影部分的面积．

连接AC交BD于O，如图所示：

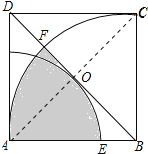
∵四边形ABCD是正方形，

∴OA=OB=BD，AC⊥BD，∠BAD=90°，AB=AD=2，∠BAO=∠ABF=45°，

∴BD==，

∴OA=OB=，

∴△AOB的面积=××=1，

∵以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切，AC⊥BD，

∴O为切点，

∵扇形AOE的面积=，扇形ABF的面积=，

∴图中阴影部分的面积=.

故选D．