题目内容
1.(1)计算:$\frac{1}{x-2}$-$\frac{4}{{x}^{2}-4}$(2)先化简,再求值:1-$\frac{a-2}{a}$÷$\frac{{a}^{2}-4}{{a}^{2}+a}$,其中a=-$\frac{2}{3}$.
分析 (1)根据分式的除法可以解答本题;
(2)先化简题目中的式子,然后将a的值代入化简后的式子即可解答本题.
解答 解:(1)$\frac{1}{x-2}$-$\frac{4}{{x}^{2}-4}$
=$\frac{(x+2)-4}{(x-2)(x+2)}$
=$\frac{x-2}{(x-2)(x+2)}$
=$\frac{1}{x+2}$;
(2)1-$\frac{a-2}{a}$÷$\frac{{a}^{2}-4}{{a}^{2}+a}$
=1-$\frac{a-2}{a}•\frac{a(a+1)}{(a+2)(a-2)}$
=1-$\frac{a+1}{a+2}$
=$\frac{a+2-a-1}{a+2}$
=$\frac{1}{a+2}$,
当a=-$\frac{2}{3}$时,原式=$\frac{1}{-\frac{2}{3}+2}$=$\frac{1}{\frac{4}{3}}$=$\frac{3}{4}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
9.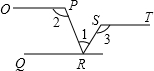 如图,已知OP∥QR∥ST,则下列等式中正确的是( )
如图,已知OP∥QR∥ST,则下列等式中正确的是( )
 如图,已知OP∥QR∥ST,则下列等式中正确的是( )
如图,已知OP∥QR∥ST,则下列等式中正确的是( )| A. | ∠1+∠2-∠3=90° | B. | ∠1-∠2+∠3=180° | C. | ∠2+∠3-∠1=180° | D. | ∠1+∠2+∠3=180° |
6.计算$\frac{1}{3}$a2•(-6ab)的结果正确的是( )
| A. | -2a2b | B. | 2a2b | C. | -2a3b | D. | 2a3b |
11.某自行车厂一周计划生产700辆自行车,平均每天生产自行车100辆,由于各种原因,实际每天生产量与计划每天生产量相比有出入.表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆):
(1)根据记录可知前三天共生产自行车303辆;
(2)产量最多的一天比产量最少的一天多生产27 辆;
(3)若该厂实行按生产的自行车数量的多少计工资,即计件工资制.如果每生产一辆自行车就可以得人民币60元,超额完成任务,每超一辆可多得15元;若不足计划数的,每少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +8 | -2 | -3 | +16 | -9 | +10 | -11 |
(2)产量最多的一天比产量最少的一天多生产27 辆;
(3)若该厂实行按生产的自行车数量的多少计工资,即计件工资制.如果每生产一辆自行车就可以得人民币60元,超额完成任务,每超一辆可多得15元;若不足计划数的,每少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
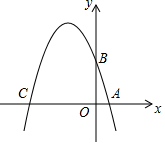 如图,在平面直角坐标系xOy中,A、B、C三点分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.
如图,在平面直角坐标系xOy中,A、B、C三点分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.