题目内容
10．
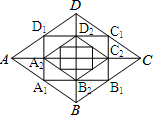如图，菱形ABCD的对角线长分别为a、b，以菱形ABCD各边的中点为顶点作矩形A1B1C1D1，然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2，…，如此下去，得到四边形A2011B2011C2011D2011的面积用含a，b的代数式表示为$\frac{ab}{{2}^{2012}}$．
分析 根据三角形中位线定理，逐步推理出各小长方形的面积，总结出规律，用规律解答即可．
解答 解：∵四边形ABCD中，AC=a，BD=b，且AC丄BD，
∴S四边形ABCD=ab÷2；
由三角形的中位线的性质可以推知，每得到一次四边形，它的面积变为原来的一半，
四边形AnBnCnDn的面积是 $\frac{ab}{{2}^{n+1}}$．
则四边形A2011B2011C2011D2011面积=$\frac{ab}{{2}^{2012}}$．
故答案是：$\frac{ab}{{2}^{2012}}$．
点评 此题主要考查学生对菱形的性质及三角形中位线定理的理解及运用．此题难度适中，注意数形结合思想的应用．
练习册系列答案
相关题目
如图所示，一个不等式组的解集表示在数轴上，这个不等式组可能是$\left\{\begin{array}{l}{x≤3}\\{x＞-1}\end{array}\right.$．
15．某校准备组织520名学生进行野外考察活动，行李共有240件．学校计划租用甲、乙两种型号的汽车共12辆，经了解，甲种汽车每辆最多能载50人和15件行李，乙种汽车每辆最多能载40人和25件行李．设租用甲种汽车x辆，你认为下列符合题意的不等式组是（ ）
| A． | $\left\{\begin{array}{l}{50x+40（12-x）≥520}\\{15x+25（12-x）≥240}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{50x+40（12-x）＞520}\\{15x+25（12-x）＞240}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{50x+40（12-x）≤520}\\{15x+25（12-x）≤240}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{50x+40（12-x）＜520}\\{15x+25（12-x）＜240}\end{array}\right.$ |
2．
如图把两个不等式的解集表示在数轴上，则这两个不等式组成的不等式组可能是（ ）
如图把两个不等式的解集表示在数轴上，则这两个不等式组成的不等式组可能是（ ）| A． | $\left\{\begin{array}{l}{x＜4}\\{x≥-1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x＞4}\\{x≤1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x＞4}\\{x＞-1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x≤4}\\{x＞-1}\end{array}\right.$ |
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：