题目内容
8．
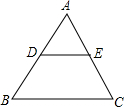如图，D、E分别是△ABC两边的中点，△ADE的面积记为S1，四边形DBCE的面积记为S2，则下列结论正确的是（ ）| A． | S1=S2 | B． | S2=2S1 | C． | S2=3S1 | D． | S2=4S1 |
分析 由已知可知DE是△ABC的中位线，那么DE∥BC，再根据平行线分线段成比例定理的推论，可得△ADE∽△ABC，且相似比等于1：2，则面积比等于1：4，从而可求四边形DBCE的面积和△ADE的面积的关系．
解答 解：∵D、E是△ABC两边AB、AC的中点，
∴△ADE∽△ABC，相似比为1：2，
∴S△ADE：S△ABC=1：4，
∴S△DBCE：S△ADE=3：1，
故选C．
点评 本题比较简单，考查的是三角形的中位线定理及相似三角形的性质．
练习册系列答案
相关题目
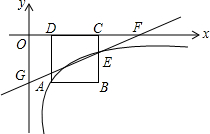如图，正方形ABCD的顶点C，D在x轴的正半轴上，反比例函数y=$\frac{k}{x}$（k≠0）在第四象限的图象经过顶点A（m，-2）和BC边上的点E（n，-$\frac{2}{3}$），过点E的直线l交x轴于点F，交y轴于点G（0，-2），则点F的坐标是（$\frac{9}{2}$，0）．
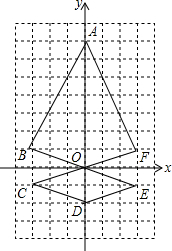如图，在8×12的网格图中（每个小正方形的边长均为1个单位）中有一个风筝的图案，以字母O为原点建立直角坐标系．
16．在平面直角坐标系中，点P（3，2）在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
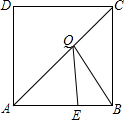如图，在边长为4的正方形ABCD中，E是AB边上的一点，且AE=3，点Q为对角线AC上的动点，如果直角三角形斜边的平方等于两条直角边的平方和，那么是否可求出△BEQ周长的最小值．
18．
下列四个图形中，由题图经过平移得到的图形是（ ）
下列四个图形中，由题图经过平移得到的图形是（ ）| A． |  | B． |  | C． |  | D． |  |