题目内容
3.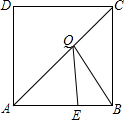 如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,如果直角三角形斜边的平方等于两条直角边的平方和,那么是否可求出△BEQ周长的最小值.
如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,如果直角三角形斜边的平方等于两条直角边的平方和,那么是否可求出△BEQ周长的最小值.
分析 由正方形的性质得出点B与点D关于直线AC对称,∠DAE=90°,得出DE的长即为DQ+QE的最小值,由勾股定理求出DE,即可得出结果.
解答 解:连接BD、DE,如图所示:
∵四边形ABCD是正方形,
∴点B与点D关于直线AC对称,∠DAE=90°,AB=AD=4,
∴DE的长即为DQ+QE的最小值,BE=1,
∵DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴△BEQ的最小值=5+1=6.
点评 本题考查了正方形的性质、最小值问题、勾股定理、轴对称的性质;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
18.已知反比例函数y=$\frac{2}{x}$,在下列结论中,不正确的是( )
| A. | 图象必经过点(1,2) | B. | y随x的增大而减少 | ||
| C. | 图象在第一、三象限 | D. | 若x>1,则y<2 |
8.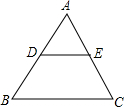 如图,D、E分别是△ABC两边的中点,△ADE的面积记为S1,四边形DBCE的面积记为S2,则下列结论正确的是( )
如图,D、E分别是△ABC两边的中点,△ADE的面积记为S1,四边形DBCE的面积记为S2,则下列结论正确的是( )
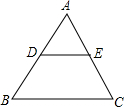 如图,D、E分别是△ABC两边的中点,△ADE的面积记为S1,四边形DBCE的面积记为S2,则下列结论正确的是( )
如图,D、E分别是△ABC两边的中点,△ADE的面积记为S1,四边形DBCE的面积记为S2,则下列结论正确的是( )| A. | S1=S2 | B. | S2=2S1 | C. | S2=3S1 | D. | S2=4S1 |
15.“江阴市明天降水概率是20%”,对此消息下列说法中正确的是( )
| A. | 江阴市明天将有20%的地区降水 | B. | 江阴市明天将有20%的时间降水 | ||
| C. | 江阴市明天降水的可能性较小 | D. | 江阴市明天肯定不降水 |
12.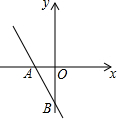 如图所示,一次函数y=(m-2)x-4的图象分别与x轴、y轴的负半轴相交于A,B,则m的取值范围是( )
如图所示,一次函数y=(m-2)x-4的图象分别与x轴、y轴的负半轴相交于A,B,则m的取值范围是( )
 如图所示,一次函数y=(m-2)x-4的图象分别与x轴、y轴的负半轴相交于A,B,则m的取值范围是( )
如图所示,一次函数y=(m-2)x-4的图象分别与x轴、y轴的负半轴相交于A,B,则m的取值范围是( )| A. | m>2 | B. | m<2 | C. | m>0 | D. | m<0 |
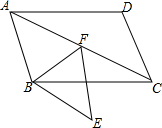 如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.
如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB. 定义{A,B,C}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x-3的“特征数”是{1,-2,-3},函数y=2x+4的“特征数”是{0,2,4},函数y=-x的“特征数”是{0,-1,0}.
定义{A,B,C}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x-3的“特征数”是{1,-2,-3},函数y=2x+4的“特征数”是{0,2,4},函数y=-x的“特征数”是{0,-1,0}.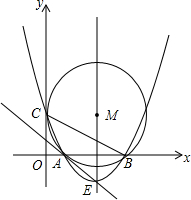 如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A,B两点.
如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A,B两点.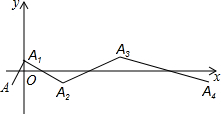 如图,一个动点A在平面直角坐标系中作折线运动,第一次从点(-1,-1)到A1(0,1),第二次运动到A2(3,-1),第三次运动到A3(8,1),第四次运动到A4(15,-1)…,按这样的运动规律,经过第11次运动后,动点A11的坐标是(120,1).
如图,一个动点A在平面直角坐标系中作折线运动,第一次从点(-1,-1)到A1(0,1),第二次运动到A2(3,-1),第三次运动到A3(8,1),第四次运动到A4(15,-1)…,按这样的运动规律,经过第11次运动后,动点A11的坐标是(120,1).