题目内容
已知a、b、c为△ABC的三边长，且a+b+c=36，
=
=
，求△ABC三边的长．
| a |
| 3 |
| b |
| 4 |
| c |
| 5 |
考点：比例的性质
专题：
分析：根据比例的性质，可得a、b、c的关系，根据a、b、c的关系，可得一元一次方程，根据解方程，可得答案．
解答：解：
=
=
，得
a=
c，b=
c，
把a=
c，b=
c代入且a+b+c=36，得
c+
c+c=36，
解得c=15，
a=
c=9，
b=
c=12，
△ABC三边的长：a=9，b=12，c=15．
| a |
| 3 |
| b |
| 4 |
| c |
| 5 |
a=
| 3 |
| 5 |
| 4 |
| 5 |
把a=
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
解得c=15，
a=
| 3 |
| 5 |
b=
| 4 |
| 5 |
△ABC三边的长：a=9，b=12，c=15．
点评：本题考查了比例的性质，利用了比例的性质．
练习册系列答案
相关题目
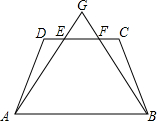如图，在等腰梯形ABCD中，AB∥DC，线段AG，BG分别交CD于点E，F，DE=CF．试判断△GAB的形状，并说明理由．
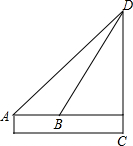小明想测量CD的高度，他在A处仰望塔顶，仰角为45°，再往塔的方向前进50m至B处，测得仰角为60°，小明身高为1.5m，那么该塔有多高？