Question

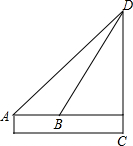小明想测量CD的高度，他在A处仰望塔顶，仰角为45°，再往塔的方向前进50m至B处，测得仰角为60°，小明身高为1.5m，那么该塔有多高？

Answer 1

考点：解直角三角形的应用-仰角俯角问题

专题：

分析：设CD=x，在Rt△AED中求出AE，在Rt△DBE中求出BE，再由AE=50m，可求出x的值，再由CD=DE+EC即可得出答案．

解答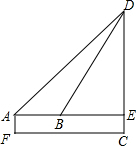：解：设DE=x，
在Rt△AED中，ED=x，∠DAE=45°，
则tan45°=

DE

AE

=

x

AE

=1
故AE=DE=x，
在Rt△DBE中，ED=x，∠DBE=60°，
则tan60°=

DE

BE

=

x

BE

=

3

，
故BE=

3

3

x，
由题意得，AB=AE-BE=x-

3

3

x=50，
解得：x=75+25

3

，
则这棵树的高度=75+25

3

+1.5≈76.5+25

3

（m）．
答：塔高为76.5+25

3

 m．

点评：本题考查了解直角三角形的应用，解答本题关键是构造直角三角形，利用三角函数的知识表示出相关线段的长度．