题目内容
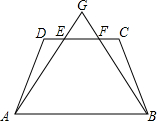如图，在等腰梯形ABCD中，AB∥DC，线段AG，BG分别交CD于点E，F，DE=CF．试判断△GAB的形状，并说明理由．考点：等腰梯形的性质
专题：
分析：根据等腰梯形的性质得出∠D=∠C，证△ADE≌△BCF，推出AE=BF，∠DEA=∠CFB，求出∠GEF=∠GFE，推出GE=GF即可．
解答：解：△GAB是等腰三角形，
理由是：∵在等腰梯形ABCD中，AB∥DC，
∴∠D=∠C，
在△ADE和△BCF中
∴△ADE≌△BCF，
∴AE=BF，∠DEA=∠CFB，
∵∠DEF=∠DEA，∠GFE=∠CFB，
∴∠GEF=∠GFE，
∴GE=GF，
∵AE=BF，
∴GA=GB，
∴△GAB是等腰三角形．
理由是：∵在等腰梯形ABCD中，AB∥DC，
∴∠D=∠C，
在△ADE和△BCF中
|
∴△ADE≌△BCF，
∴AE=BF，∠DEA=∠CFB，
∵∠DEF=∠DEA，∠GFE=∠CFB，
∴∠GEF=∠GFE，
∴GE=GF，
∵AE=BF，
∴GA=GB，
∴△GAB是等腰三角形．
点评：本题考查了等腰梯形的性质，等腰三角形的判定，全等三角形的性质和判定等知识点的应用，主要考查学生的推理能力．
练习册系列答案
相关题目
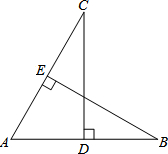如图，D、E分别是AB、AC的中点，CD⊥AB于D，BE⊥AC于E．
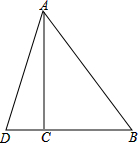有一块直角三角形绿地ABC，∠ACB=90°，经测量AC=80m，BC=60m，现计划将绿地扩展为以AB为一条边的等腰△ABD，且D点在线段BC的延长线上，求扩展后绿地的面积．
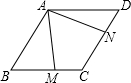如图，在?ABCD中，∠ABC=60°，且AB=BC，∠MAN=60°，请探索BM，DN与AB的数量关系，并证明你的结论．