题目内容
3.化简求值:$\frac{2x-4}{x-3}÷(-\frac{5}{x-3}-x-3)$,其中x=-1.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{2(x-2)}{x-3}$÷(-$\frac{5-{x}^{2}+9}{x-3}$)
=$\frac{2(x-2)}{x-3}$÷$\frac{4-{x}^{2}}{x-3}$
=$\frac{2(x-2)}{x-3}$•$\frac{x-3}{-(x+2)(x-2)}$
=-$\frac{2}{x+2}$,
当x=-1时,原式=-$\frac{2}{-1+2}$=-2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
14.下列根据等式的性质变形正确的是( )
| A. | 由4x=2x-1,得4x-2x=1 | B. | 由-2x=4,得x=2 | ||
| C. | 由5x-3=4,得5x=4-3 | D. | 由-3x-2=2x+3,得-3x-2x=3+2 |
18.在某中学开展的“书香伴我行”读书活动中,为了解九年级300名学生一个月的读书情况,随机调查了九年级50名学生读书的册数,统计数据如表所示:
估计这所中学九年级学生一个月共读书约648册,你的估计理由是50名学生读书的平均册数等于全年级学生读书的册数.
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 13 | 16 | 17 | 3 |
8. 如图所示,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
如图所示,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
 如图所示,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
如图所示,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )| A. | $\frac{3}{2}$ | B. | 4 | C. | $\frac{5}{2}$ | D. | 1 |
13.汽车从车站出发向东行驶150米,向西行驶60米,又继续向东行200米,那么汽车现在的位置是( )
| A. | 车站以东290米 | B. | 车站以西410米 | C. | 车站以东410米 | D. | 车站以西290米 |
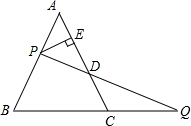 如图,P是等边△ABC的AB边上一点,过P作PE⊥AC于E,在BC的延长线上截取CQ=AP,连接PQ交AC于点D.
如图,P是等边△ABC的AB边上一点,过P作PE⊥AC于E,在BC的延长线上截取CQ=AP,连接PQ交AC于点D.