题目内容
5.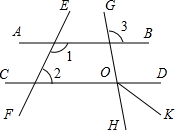 已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH.
已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH.(1)直线AB与CD有怎样的位置关系?说明理由;
(2)∠DOK的度数是多少?
分析 (1)由同旁内角互补两直线平行可判定AB∥CD;
(2)由条件结合平行线的性质可求得∠GOD,再结合角平分线的定义可求得∠DOK.
解答 解:
(1)AB∥CD,
理由如下:
∵∠1+∠2=180°,
∴AB∥CD;
(2)∵AB∥CD,∠3=100°,
∴∠GOD=∠3=100°,
∵∠GOD+∠DOH=180°,
∴∠DOH=80°,
∵OK平分∠DOH,
∴∠DOK=$\frac{1}{2}$∠DOH=40°.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
5.阿联抛一枚质地均匀的硬币,连续抛3次,硬币均正面朝上落地,如果他再抛第4次,那么硬币正面朝上的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 1 |
 如图,用A类、B类、C类卡片若干张,拼成一个长为2a+3b,宽为a+2b的矩形,则分别需要A类卡片2张,B类卡片7张,C类卡片6张.
如图,用A类、B类、C类卡片若干张,拼成一个长为2a+3b,宽为a+2b的矩形,则分别需要A类卡片2张,B类卡片7张,C类卡片6张.
 如图,为修通铁路凿通隧道AC,量出∠C=90°,AB=5km,BC=4km,若每天凿隧道0.15km,问几天才能把隧道AC凿通?
如图,为修通铁路凿通隧道AC,量出∠C=90°,AB=5km,BC=4km,若每天凿隧道0.15km,问几天才能把隧道AC凿通?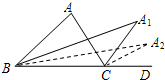 如图,已知△ABC的内角∠A=a,分别作内角∠ABC与外角∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…以此类推得到∠A2016,则∠A2016的度数是$\frac{α}{{2}^{2016}}$.
如图,已知△ABC的内角∠A=a,分别作内角∠ABC与外角∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…以此类推得到∠A2016,则∠A2016的度数是$\frac{α}{{2}^{2016}}$.