题目内容
15.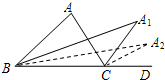 如图,已知△ABC的内角∠A=a,分别作内角∠ABC与外角∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…以此类推得到∠A2016,则∠A2016的度数是$\frac{α}{{2}^{2016}}$.
如图,已知△ABC的内角∠A=a,分别作内角∠ABC与外角∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…以此类推得到∠A2016,则∠A2016的度数是$\frac{α}{{2}^{2016}}$.
分析 根据角平分线的定义可得∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,整理即可求出∠A1的度数,同理求出∠A2,可以发现后一个角等于前一个角的$\frac{1}{2}$,根据此规律即可得解.
解答 解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠ABC+∠A1,
∴∠A1=$\frac{1}{2}$∠A,
∵∠A=α,
∴∠A1=$\frac{α}{2}$;
同理可得∠A2=$\frac{1}{2}$∠A1=$\frac{1}{2}$•$\frac{1}{2}$α=$\frac{α}{{2}^{2}}$,
∴∠An=$\frac{α}{{2}^{n}}$,
∴∠A2016=$\frac{α}{{2}^{2016}}$.
故答案为:$\frac{α}{{2}^{2016}}$
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.当x=7与x=-7时,代数式3x4-2x2+1的两个值( )
| A. | 相等 | B. | 互为倒数 | ||
| C. | 互为相反数 | D. | 既不相等也不互为相反数 |
7.在一张挂历上,任意圈出同一列上的三个数的和不可能是( )
| A. | 14 | B. | 33 | C. | 66 | D. | 69 |
5.已知下列各式:abc,2πR,x+3y,0,$\frac{x-y}{2}$,其中单项式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
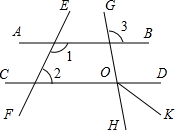 已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH.
已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH. 如图.
如图.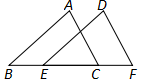 如图,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF,AB=DE.
如图,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF,AB=DE.