题目内容
10.如图(a),已知∠BAG+∠AGD=180°,AE、EF、EG是三条折线段.(1)若∠E=∠F,如图(b)所示,求证:∠1=∠2;
(2)根据图(a),写出∠1+∠E与∠2+∠F之间的关系,不需证明.

分析 (1)由∠E=∠F可知AF∥EG,又因为∠BAG+∠AGD=180°,所以AB∥CD,利用内错角相等即可求证;
(2)利用对顶角相等即可得出:∠E+∠EGA=∠F+∠GAF,利用平行线的性质即可求出∠1+∠E与∠2+∠F之间的关系;
解答 解:(1)∵∠BAG+∠AGD=180°,
∴AB∥CD,
∴∠BAG=∠AGC,
∵∠E=∠F,
∴AF∥EG,
∴∠FAG=∠AGE,
∴∠BAG-∠FAG=∠AGC-∠AGE
∴∠1=∠2,
(2)由(1)可知:AB∥CD,
∴∠1+∠GAF=∠2+∠EGA,
∵∠E+∠EGA=∠F+∠GAF,
∴上述两式相加得:∴∠1+∠GAF+∠E+∠EGA=∠2+∠EGA+∠F+∠GAF
∴∠1+∠E=∠2+∠F;
点评 本题考查平行线的性质与判定,要注意观察同位角、内错角、同旁内角.

练习册系列答案
相关题目
12.方程3x2+1=6x的二次项系数和一次项系数分别为( )
| A. | 3和6 | B. | 3和-6 | C. | 3和-1 | D. | 3和1 |
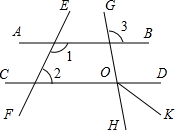 已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH.
已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH.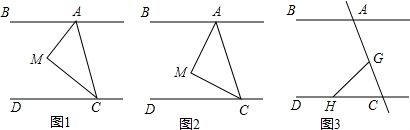
 有一个英文单词的字母顺序对应如图中的有序数对分别为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来或者翻译成中文为study(学习).
有一个英文单词的字母顺序对应如图中的有序数对分别为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来或者翻译成中文为study(学习).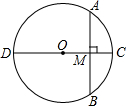 如图,⊙O的直径CD垂直弦AB于M,且M是半径OC的中点,AB=6,则半径OA的长是?
如图,⊙O的直径CD垂直弦AB于M,且M是半径OC的中点,AB=6,则半径OA的长是?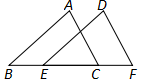 如图,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF,AB=DE.
如图,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF,AB=DE.