题目内容
(1)如图,CA=CD,∠1=∠2,BC=EC.求证:AB=DE.
(2)如图,已知点A(-3,4),B(-3,0),将△OAB绕原点O顺时针旋转90°,得到△OA1B1.
①画出△OA1B1,并直接写出点A1、B1的坐标;
②求出旋转过程中点A所经过的路径长(结果保留π).

(2)如图,已知点A(-3,4),B(-3,0),将△OAB绕原点O顺时针旋转90°,得到△OA1B1.
①画出△OA1B1,并直接写出点A1、B1的坐标;
②求出旋转过程中点A所经过的路径长(结果保留π).

考点:作图-旋转变换,全等三角形的判定与性质,弧长的计算
专题:
分析:(1)根据∠1=∠2,可得出∠BCA=∠ECD,然后利用SAS证明△ABC≌△DEC,继而可得出AB=DE;
(2)①分别作出A、B绕点O顺时针旋转90°后的点A1、B1,然后顺次连接A1B1、A1O、B1O,并写出点A1、B1的坐标;
②点A的路径为以OA为半径的弧长,根据弧长公式计算即可.
(2)①分别作出A、B绕点O顺时针旋转90°后的点A1、B1,然后顺次连接A1B1、A1O、B1O,并写出点A1、B1的坐标;
②点A的路径为以OA为半径的弧长,根据弧长公式计算即可.
解答:(1)证明:∵∠1=∠2,
∴∠1+∠ECA=∠2+∠ECA,
即∠ACB=∠DCE,
在△ABC和△DEC中,
,
∴△ABC≌△DEC(SAS),
∴AB=DE.
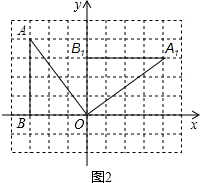
(2)解:①如图所示:
A1(4,3),B1(0,3);
②如图,在Rt△OAB中,
∵OB2+AB2=OA2,
∴OA=
=5,
∴l=
=
,
因此点A所经过的路径长为
.
∴∠1+∠ECA=∠2+∠ECA,
即∠ACB=∠DCE,
在△ABC和△DEC中,
|
∴△ABC≌△DEC(SAS),
∴AB=DE.

(2)解:①如图所示:
A1(4,3),B1(0,3);
②如图,在Rt△OAB中,
∵OB2+AB2=OA2,
∴OA=
| 32+42 |
∴l=
| 90×5π |
| 180 |
| 5π |
| 2 |
因此点A所经过的路径长为
| 5π |
| 2 |
点评:本题考查了全等三角形的判定与性质以及根据旋转变换作图,解答本题的关键是作出各点旋转后的对应点.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,⊙O的半径是5,sinB=
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,⊙O的半径是5,sinB=| 2 |
| 5 |
| A、2 | B、3 | C、4 | D、5 |
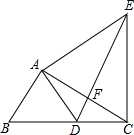 如图,把△ABC绕点A旋转得到△ADE(D与E重合),当点D刚好落在BC上时,连接CE,设AC、DE相交于点F,则图中相似三角形的对数是( )
如图,把△ABC绕点A旋转得到△ADE(D与E重合),当点D刚好落在BC上时,连接CE,设AC、DE相交于点F,则图中相似三角形的对数是( )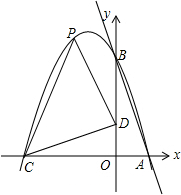 如图,在直角坐标系中,直线y=-4x+4交坐标轴于点A、B,如图所示.将△AOB绕原点O逆时针旋转90°,得到△DOC.抛物线y=ax2+bx+c经过点A、B、C.
如图,在直角坐标系中,直线y=-4x+4交坐标轴于点A、B,如图所示.将△AOB绕原点O逆时针旋转90°,得到△DOC.抛物线y=ax2+bx+c经过点A、B、C.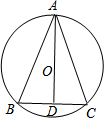 如图,已知AD既是△ABC的中线,又是角平分线,请判断:
如图,已知AD既是△ABC的中线,又是角平分线,请判断: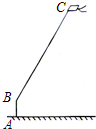 周末,小强在文化广场放风筝.如图,小强为了计算风筝离地面的高度,他测得风筝的仰角为58°,已知风筝线BC的长为10米,小强的身高AB为1.55米.请你帮小强画出测量示意图,并计算出风筝离地面的高度(结果精确到0.1米).(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
周末,小强在文化广场放风筝.如图,小强为了计算风筝离地面的高度,他测得风筝的仰角为58°,已知风筝线BC的长为10米,小强的身高AB为1.55米.请你帮小强画出测量示意图,并计算出风筝离地面的高度(结果精确到0.1米).(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)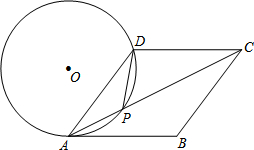 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.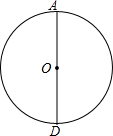 在学习圆与正多边形时,马露、高静两位同学设计了一个画圆内接正三角形的方法:
在学习圆与正多边形时,马露、高静两位同学设计了一个画圆内接正三角形的方法: