题目内容
如图，⊙O是△ABC的外接圆，AD是⊙O的直径，⊙O的半径是5，sinB=| 2 |
| 5 |
| A、2 | B、3 | C、4 | D、5 |
考点：圆周角定理,锐角三角函数的定义
专题：
分析：首先连接CD，由AD是⊙O的直径，可得∠ACD=90°，又由⊙O的半径是5，sinB=
，即可求得答案．
| 2 |
| 5 |
解答：
解：连接CD，
∵AD是⊙O的直径，
∴∠ACD=90°，
∵⊙O的半径是5，
∴AD=10，
∵∠B=∠D，sinB=
，
∴sinD=
=
，
∴AC=4．
故选C．
解：连接CD，∵AD是⊙O的直径，
∴∠ACD=90°，
∵⊙O的半径是5，
∴AD=10，
∵∠B=∠D，sinB=
| 2 |
| 5 |
∴sinD=
| AC |
| AD |
| 2 |
| 5 |
∴AC=4．
故选C．
点评：此题考查了圆周角定理以及三角函数的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
对于反比例函数y=
（k≠0），下列说法错误的是（ ）
| k2 |
| x |
| A、它的图象分布在第一、三象限 |
| B、y随x的增大而减小 |
| C、它的图象是中心对称图形 |
| D、点（k，k）在它的图象上 |
若有理数a和b在数轴上所表示的点分别在原点的右边和左边，则
-|a-b|等于（ ）
| b2 |
| A、a | B、-a |
| C、2b+a | D、2b-a |
下列运算正确的是（ ）
| A、x+x2=x3 |
| B、（-2a）2=2a2 |
| C、（x2）3=x5 |
| D、x5÷x3=x2 |
计算（a3b）2的结果是（ ）
| A、a6b |
| B、a6b2 |
| C、a5b2 |
| D、a3b2 |
方程组
的解是（ ）
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
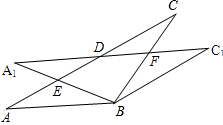如图，在等腰△ABC中，AB=BC，∠A=30°将△ABC绕点B顺时针旋转30°，得△A1BC1，A1B交AC于点E，A1C1分别交AC、BC于D、F两点．