题目内容
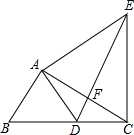 如图,把△ABC绕点A旋转得到△ADE(D与E重合),当点D刚好落在BC上时,连接CE,设AC、DE相交于点F,则图中相似三角形的对数是( )
如图,把△ABC绕点A旋转得到△ADE(D与E重合),当点D刚好落在BC上时,连接CE,设AC、DE相交于点F,则图中相似三角形的对数是( )| A、3对 | B、4对 | C、5对 | D、6对 |
考点:相似三角形的判定
专题:常规题型
分析:根据旋转的性质得到△ABC≌△ADE,∠2=∠1,利用三角形内角和得到∠3=∠4,则可判断△AFE∽△DFC;根据相似的性质得AF:DF=EF:FC,而∠AFD=∠EFC,则可判断△AFD∽△EFC;由于∠BAC=∠DAE,AB=AD,AC=AE,所以∠3=∠5,于是可判断△ABD∽△AEC.
解答: 解:∵把△ABC绕点A旋转得到△ADE(D与E重合),
解:∵把△ABC绕点A旋转得到△ADE(D与E重合),
∴△ABC≌△ADE,∠2=∠1,
∴∠3=∠4,
∴△AFE∽△DFC;
∴AF:DF=EF:FC,
而∠AFD=∠EFC,
∴△AFD∽△EFC;
∵把△ABC绕点A旋转得到△ADE(D与E重合),
∴∠BAC=∠DAE,AB=AD,AC=AE,
∴∠3=∠5,
∴△ABD∽△AEC.
故选B.
 解:∵把△ABC绕点A旋转得到△ADE(D与E重合),
解:∵把△ABC绕点A旋转得到△ADE(D与E重合),∴△ABC≌△ADE,∠2=∠1,
∴∠3=∠4,
∴△AFE∽△DFC;
∴AF:DF=EF:FC,
而∠AFD=∠EFC,
∴△AFD∽△EFC;
∵把△ABC绕点A旋转得到△ADE(D与E重合),
∴∠BAC=∠DAE,AB=AD,AC=AE,
∴∠3=∠5,
∴△ABD∽△AEC.
故选B.
点评:本题考查了相似三角形的判定:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;三组对应边的比相等的两个三角形相似;两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对于反比例函数y=
(k≠0),下列说法错误的是( )
| k2 |
| x |
| A、它的图象分布在第一、三象限 |
| B、y随x的增大而减小 |
| C、它的图象是中心对称图形 |
| D、点(k,k)在它的图象上 |
下面计算正确的是( )
(1)a2+a3=a5;(2)x3•x3=x9;(3)y4•y4=y8; (4)100•103=105.
(1)a2+a3=a5;(2)x3•x3=x9;(3)y4•y4=y8; (4)100•103=105.
| A、(1)、(2) |
| B、(2)、(3) |
| C、(3)、(4) |
| D、(1)、(4) |
下列说法不正确的是( )
A、
| ||||
| B、-9是81的一个平方根 | ||||
| C、0.2的算术平方根是0.04 | ||||
| D、-27的立方根是-3 |
 如图,AB是⊙O的弦,OC⊥AB于点C,若AB=16cm,OC=6cm,则⊙O的半径为( )
如图,AB是⊙O的弦,OC⊥AB于点C,若AB=16cm,OC=6cm,则⊙O的半径为( )| A、3cm | B、5cm |
| C、6cm | D、10cm |
若有理数a和b在数轴上所表示的点分别在原点的右边和左边,则
-|a-b|等于( )
| b2 |
| A、a | B、-a |
| C、2b+a | D、2b-a |
下列运算正确的是( )
| A、x+x2=x3 |
| B、(-2a)2=2a2 |
| C、(x2)3=x5 |
| D、x5÷x3=x2 |
 如图,Rt△ABC中,∠C=90°,D是BC上一点,AD=BD,tan∠ADC=
如图,Rt△ABC中,∠C=90°,D是BC上一点,AD=BD,tan∠ADC=