题目内容
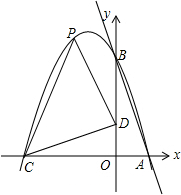 如图,在直角坐标系中,直线y=-4x+4交坐标轴于点A、B,如图所示.将△AOB绕原点O逆时针旋转90°,得到△DOC.抛物线y=ax2+bx+c经过点A、B、C.
如图,在直角坐标系中,直线y=-4x+4交坐标轴于点A、B,如图所示.将△AOB绕原点O逆时针旋转90°,得到△DOC.抛物线y=ax2+bx+c经过点A、B、C.(1)直接写出点C、D的坐标;
(2)求抛物线的解析式;
(3)点P是第二象限内抛物线上的动点,求△PCD面积的最大值.
考点:二次函数综合题
专题:
分析:(1)首先求出A和B点的坐标,由旋转的性质可知OA=OD,OB=OC,继而求出点C、D的坐标;
(2)设抛物线的解析式为y=ax2+bx+c,把A,B,C点的坐标代入求出a,b,c的值即可;
(3)先运用待定系数法求出直线CD的解析式,设PM与CD的交点为N,根据CD的解析式表示出点N的坐标,再根据S△PCD=S△PCN+S△PDN就可以表示出三角形PCD的面积,运用顶点式就可以求出结论.
(2)设抛物线的解析式为y=ax2+bx+c,把A,B,C点的坐标代入求出a,b,c的值即可;
(3)先运用待定系数法求出直线CD的解析式,设PM与CD的交点为N,根据CD的解析式表示出点N的坐标,再根据S△PCD=S△PCN+S△PDN就可以表示出三角形PCD的面积,运用顶点式就可以求出结论.
解答:解:(1)∵直线y=-4x+4交坐标轴于点A、B,
∴B点的坐标为(0,4),
设y=0,则x=1,
∴A点的坐标为(1,0),
∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,
∴△DOC≌△AOB,
∴OC=OB=4,OD=OA=1,
∴C、D的坐标分别为(-4,0),(0,1);
(2)设抛物线的解析式为y=ax2+bx+c,把A,B,C点的坐标代入得:
,
解得:
,
∴抛物线的解析式为y=-x2-3x+4;
②设直线CD的解析式为y=kx+b,由题意,得
,
解得:
,
∴直线CD的解析式为:y=
x+1.
设PM与CD的交点为N,则点N的坐标为(t,
t+1),
∴NM=
t+1.
∴PN=PM-NM=-t2-3t+4-(
t+1)=-t2-
t+3.
∵S△PCD=S△PCN+S△PDN,
∴S△PCD=
PN•CM+
PN•OM,
=
PN(CM+OM),
=
PN•OC,
=
×4(-t2-
t+3),
=-2(t+
)2+
,
∴当t=-
时,S△PCD的最大值为
.
∴B点的坐标为(0,4),
设y=0,则x=1,
∴A点的坐标为(1,0),
∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,
∴△DOC≌△AOB,
∴OC=OB=4,OD=OA=1,
∴C、D的坐标分别为(-4,0),(0,1);
(2)设抛物线的解析式为y=ax2+bx+c,把A,B,C点的坐标代入得:

|
解得:
|
∴抛物线的解析式为y=-x2-3x+4;
②设直线CD的解析式为y=kx+b,由题意,得
|
解得:
|
∴直线CD的解析式为:y=
| 1 |
| 4 |
设PM与CD的交点为N,则点N的坐标为(t,
| 1 |
| 4 |
∴NM=
| 1 |
| 4 |
∴PN=PM-NM=-t2-3t+4-(
| 1 |
| 4 |
| 13 |
| 4 |
∵S△PCD=S△PCN+S△PDN,
∴S△PCD=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 13 |
| 4 |
=-2(t+
| 13 |
| 8 |
| 361 |
| 32 |
∴当t=-
| 13 |
| 8 |
| 361 |
| 32 |
点评:本题考查了待定系数法求函数的解析式的运用,三角形的面积公式的运用,二次函数的顶点式的运用,解答本题时,先求出二次函数的解析式是关键,用函数关系式表示出△PCD的面积由顶点式求最大值是难点.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
下面计算正确的是( )
(1)a2+a3=a5;(2)x3•x3=x9;(3)y4•y4=y8; (4)100•103=105.
(1)a2+a3=a5;(2)x3•x3=x9;(3)y4•y4=y8; (4)100•103=105.
| A、(1)、(2) |
| B、(2)、(3) |
| C、(3)、(4) |
| D、(1)、(4) |
下列运算正确的是( )
| A、x+x2=x3 |
| B、(-2a)2=2a2 |
| C、(x2)3=x5 |
| D、x5÷x3=x2 |
方程组
的解是( )
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
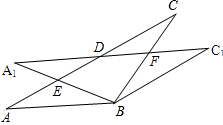 如图,在等腰△ABC中,AB=BC,∠A=30°将△ABC绕点B顺时针旋转30°,得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
如图,在等腰△ABC中,AB=BC,∠A=30°将△ABC绕点B顺时针旋转30°,得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.

 已知:如图,在平面直角坐标系xOy中,抛物线
已知:如图,在平面直角坐标系xOy中,抛物线