题目内容
如图,矩形OABC的边OA、OC分别在x轴、y轴的正半轴的正半轴上,且OA=3,OC=2,将矩形OABC向上平移4个单位得到矩形O1A1B1C1.
(1)若反比例函数y=
和y=
的图象分别经过点B、B1,求k1和k2的值;
(2)将矩形O1A1B1C1向左平移得到O2A2B2C2,当点O2、B2在反比例函数y=
的图象上时,求平移的距离和k3的值.

(1)若反比例函数y=
| k1 |
| x |
| k2 |
| x |
(2)将矩形O1A1B1C1向左平移得到O2A2B2C2,当点O2、B2在反比例函数y=
| k3 |
| x |

考点:反比例函数系数k的几何意义,平移的性质
专题:
分析:(1)将B(3,2)代入y=
,即可求出k1的值;将B1(3,6)代入y=
,即可求出k2的值;
(2)设将矩形O1A1B1C1向左平移a个单位得到O2A2B2C2,根据向左平移,横坐标相减,纵坐标不变得到点O2(-a,4),B2(3-a,6),由点O2、B2在反比例函数y=
的图象上,得出k3=-4a=6(3-a),解方程即可求出a与k3的值.
| k1 |
| x |
| k2 |
| x |
(2)设将矩形O1A1B1C1向左平移a个单位得到O2A2B2C2,根据向左平移,横坐标相减,纵坐标不变得到点O2(-a,4),B2(3-a,6),由点O2、B2在反比例函数y=
| k3 |
| x |
解答:解:(1)∵矩形OABC的边OA、OC分别在x轴、y轴的正半轴的正半轴上,且OA=3,OC=2,
∴B(3,2),
∵反比例函数y=
的图象分别经过点B,
∴k1=3×2=6;
∵将矩形OABC向上平移4个单位得到矩形O1A1B1C1,
∴B1(3,6),
∵反比例函数y=
的图象经过点B1,
∴k2=3×6=18;
(2)设将矩形O1A1B1C1向左平移a个单位得到O2A2B2C2,则O2(-a,4),B2(3-a,6),
∵点O2、B2在反比例函数y=
的图象上,
∴k3=-4a=6(3-a),
解得a=9,k3=-36.
∴B(3,2),
∵反比例函数y=
| k1 |
| x |
∴k1=3×2=6;
∵将矩形OABC向上平移4个单位得到矩形O1A1B1C1,
∴B1(3,6),
∵反比例函数y=
| k2 |
| x |
∴k2=3×6=18;
(2)设将矩形O1A1B1C1向左平移a个单位得到O2A2B2C2,则O2(-a,4),B2(3-a,6),
∵点O2、B2在反比例函数y=
| k3 |
| x |
∴k3=-4a=6(3-a),
解得a=9,k3=-36.
点评:本题考查了反比例函数比例系数k的几何意义,反比例函数图象上点的坐标特征,平移的性质,难度适中.利用数形结合与方程思想是解题的关键.

练习册系列答案
相关题目
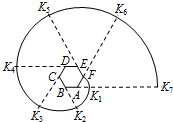 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中FK1,K1K2,K2K3,K3K4,K5K6…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2014等于( )
如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中FK1,K1K2,K2K3,K3K4,K5K6…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2014等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知反比例函数图象经过点(2,-2),(-1,n),则n等于( )
| A、3 | B、4 | C、-3 | D、-4 |
 某旅游观光车在距指挥中心90km的草原上出现故障,指挥中心得到消息后派出巡逻车前往接应,同时游客们沿着指挥中心的方向步行.巡逻车接走第一批游客到达指挥中心后,立即原速原路返回接应第二批游客,第二批游客在此期间继续原速步行.如图为游客与巡逻车距出事地点的路程y(km)和时间x(h)之间的函数图象.求巡逻车与第二批游客相遇时的距指挥中心的路程及时间.
某旅游观光车在距指挥中心90km的草原上出现故障,指挥中心得到消息后派出巡逻车前往接应,同时游客们沿着指挥中心的方向步行.巡逻车接走第一批游客到达指挥中心后,立即原速原路返回接应第二批游客,第二批游客在此期间继续原速步行.如图为游客与巡逻车距出事地点的路程y(km)和时间x(h)之间的函数图象.求巡逻车与第二批游客相遇时的距指挥中心的路程及时间.