题目内容
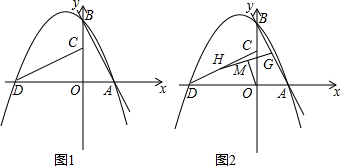
某旅游观光车在距指挥中心90km的草原上出现故障，指挥中心得到消息后派出巡逻车前往接应，同时游客们沿着指挥中心的方向步行．巡逻车接走第一批游客到达指挥中心后，立即原速原路返回接应第二批游客，第二批游客在此期间继续原速步行．如图为游客与巡逻车距出事地点的路程y（km）和时间x（h）之间的函数图象．求巡逻车与第二批游客相遇时的距指挥中心的路程及时间．考点：一次函数的应用
专题：
分析：由函数图象可以得出行人的速度为10km/h，巡逻车的速度为80km/h，就可以求出巡逻车接走第一批游客到达指挥中心的时间，就可以求出此时游客走的路程及第二批游客与指挥中心的距离，由相遇问题就可以求出巡逻车与第二批游客相遇时间和与指挥中心的距离．
解答：解：由函数图象，得
游客行走的速度为10km/h，
巡逻车的速度为80km/h，
∴巡逻车接走第一批游客到达指挥中心的时间为：
（90-10）÷80=1
∴游客行走的时间为1小时，
∴游客行走的路程为10千米．
∴第一批游客送到指挥中心后，巡逻车与第二批游客相遇的时间时为：
（90-20）÷（10+80）=
小时．
∴巡逻车与第二批游客相遇时距指挥中心的路程为：80×
=
千米．
时间为：2+
=
小时．
答：巡逻车与第二批游客相遇时距指挥中心的路程为
千米，时间为
小时．
游客行走的速度为10km/h，
巡逻车的速度为80km/h，
∴巡逻车接走第一批游客到达指挥中心的时间为：
（90-10）÷80=1
∴游客行走的时间为1小时，
∴游客行走的路程为10千米．
∴第一批游客送到指挥中心后，巡逻车与第二批游客相遇的时间时为：
（90-20）÷（10+80）=
| 7 |
| 9 |
∴巡逻车与第二批游客相遇时距指挥中心的路程为：80×
| 7 |
| 9 |
| 560 |
| 9 |
时间为：2+
| 7 |
| 9 |
| 25 |
| 9 |
答：巡逻车与第二批游客相遇时距指挥中心的路程为
| 560 |
| 9 |
| 25 |
| 9 |
点评：本题考查了一次函数的图象的性质的运用，行程问题的数量关系速度=路程÷时间的运用，相遇问题的数量关系的运用，解答时求出巡逻车和游客的速度是关键．
练习册系列答案
相关题目
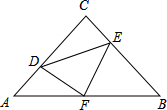如图，在等腰直角三角形ABC中，∠C=90°，AC=8，点F是AB的中点，点D、E分别在AC、BC边上运动，且始终保持DF⊥EF，则四边形CDFE的面积是在离地面高度为5米处引拉线固定电线杆，拉线与地面成60°的角，则拉线的长是（ ）
| A、10 | ||||
B、
| ||||
C、
| ||||
D、5
|
已知二次函数y=ax2+bx+c的图象如图，其对称轴x=-1，给出下列结论：①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a-b+c＜0，其中正确的结论是
