题目内容
已知反比例函数图象经过点(2,-2),(-1,n),则n等于( )
| A、3 | B、4 | C、-3 | D、-4 |
考点:反比例函数图象上点的坐标特征
专题:
分析:首先设反比例函数关系式为y=
,根据图象所经过的点可得k=2×(-2)=-4,进而得到函数解析式,再根据反比例函数图象上点的坐标特点可得n的值.
| k |
| x |
解答:解:设反比例函数关系式为y=
,
∵反比例函数图象经过点(2,-2),
∴k=2×(-2)=-4,
∴反比例函数解析式为y=-
,
∵图象经过(-1,n),
∴-1×n=-4,
解得:n=4,
故选:B.
| k |
| x |
∵反比例函数图象经过点(2,-2),
∴k=2×(-2)=-4,
∴反比例函数解析式为y=-
| 4 |
| x |
∵图象经过(-1,n),
∴-1×n=-4,
解得:n=4,
故选:B.
点评:此题主要考查了反比例函数图象上点的坐标特点,关键是掌握反比例函数图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
 已知,如图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.给出以下四个结论:①∠EBC=22.5°;②AE=2EC;③劣弧AE是劣弧DE的2倍;④DE=DC.其中不正确结论的序号是( )
已知,如图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.给出以下四个结论:①∠EBC=22.5°;②AE=2EC;③劣弧AE是劣弧DE的2倍;④DE=DC.其中不正确结论的序号是( )| A、① | B、④ | C、③ | D、② |
下列各式:
,
(a≥2),
,
,-
,其中二次根式有( )个.
| x2+1 |
| a-2 |
| (x-1)2 |
| -3 |
| x2+1 |
| A、3个 | B、4个 | C、5个 | D、6个 |
计算(-2)×(-3)的值为( )
| A、5 | B、-5 | C、6 | D、-6 |

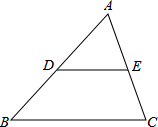 如图,在△ABC中,D、E分别为边AB、AC的中点.
如图,在△ABC中,D、E分别为边AB、AC的中点. 如图,在?ABCD中,已知点E,F分别在AB,CD上,且AE=CD.则四边形DEBF是平行四边形吗?若是,请证明.
如图,在?ABCD中,已知点E,F分别在AB,CD上,且AE=CD.则四边形DEBF是平行四边形吗?若是,请证明.