题目内容
18．
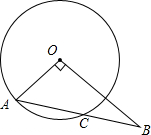如图，在Rt△A0B中，∠O=90°，OA=6，OB=8，以点O为圆心，OA为半径作圆交AB于点C，求BC的长．
分析 作OD⊥AB于D，根据勾股定理求出AB，根据三角形的面积公式求出OD，根据勾股定理求出AD，根据垂径定理求出AC，计算得到答案．
解答 解：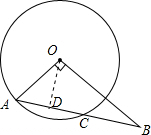
作OD⊥AB于D，
∵∠O=90°，OA=6，OB=8，
∴AB=$\sqrt{A{O}^{2}+O{B}^{2}}$=10，
∵$\frac{1}{2}$×OA×OB=$\frac{1}{2}$×AB×OD，
∴OD=4.8，
∴AD=$\sqrt{O{A}^{2}-O{D}^{2}}$=3.6，
则AC=7.2，
∴BC=AB-AC=2.8，
答BC的长为2.8．
点评 本题考查的是垂径定理和勾股定理的应用，掌握垂直于弦的直径平分弦是解题的关键．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
8．若y=2${x}^{{m}^{2}-2}$是二次函数，则m等于（ ）
| A． | -2 | B． | 2 | C． | ±2 | D． | 不能确定 |
13．△ABC和△DEF分别满足下列条件，其中△ABC与△DEF不相似的是（ ）
| A． | ∠A=∠D=45°，∠C=26°，∠E=109° | |
| B． | AB=1，AC=1.5，BC=2，DE=8，DF=12，EF=16 | |
| C． | AB=a，BC=b，AC=c，DE=$\sqrt{a}$，EF=$\sqrt{b}$，DF=$\sqrt{c}$ | |
| D． | AB=AC，DE=DF，∠A=∠D=40° |
3．若点C数线段AB的黄金分割点，且AC＞BC，则下列说法正确的有（ ）
①AB=$\frac{\sqrt{5}+1}{2}$AC；②AC=3-$\frac{3-\sqrt{5}}{2}$AB；③AB：AC=AC：AB；④AC≈0.618AB．
①AB=$\frac{\sqrt{5}+1}{2}$AC；②AC=3-$\frac{3-\sqrt{5}}{2}$AB；③AB：AC=AC：AB；④AC≈0.618AB．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
实数a，b，c在数轴上的对应点如图所示，化简a+|a+b|-|b-c|-|b+c-a|=b-a．
7．有一批袋装食品，标准质量为每袋50g，现抽取10袋样品进行检测．结果如下（单位：g）：48，51，52，49，53，52，48，49，50，52．
（1）请你用正、负数表示每袋食品与标准质量的差值，并填在表中：
（2）请你计算表中的差值的和；
（3）请你计算这10袋样品食品的总质量．
（1）请你用正、负数表示每袋食品与标准质量的差值，并填在表中：
| 袋号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 与标准质量的差值 |
（3）请你计算这10袋样品食品的总质量．