题目内容
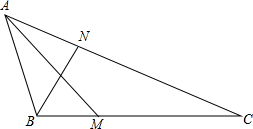 如图,在△ABC中,∠BAC=40°,∠ABC=120°,AM、BN分别为∠BAC,∠ABC的角平分线,证明:AB+AN=AM+BM.
如图,在△ABC中,∠BAC=40°,∠ABC=120°,AM、BN分别为∠BAC,∠ABC的角平分线,证明:AB+AN=AM+BM.考点:全等三角形的判定与性质
专题:证明题
分析:设AM,BN的交点为E,在MC上取MF=ME,根据角平分线定义求出∠1=∠2=20°;∠3=∠4=60°;∠7=∠8,推出∠5=∠AEN求出AE=AN,求出∠8=∠1,根据AAS推出△ABE≌△FBE,推出AB=BF即可.
解答:证明:设AM,BN的交点为E,在MC上取MF=ME,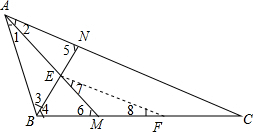
∵∠BAC=40°,∠ABC=120°AM,BN分别为∠BAC,∠ABC的角平分线
∴∠1=∠2=20°;∠3=∠4=60°;∠7=∠8
∴∠5=180°-∠BAC-∠3=80°=∠AEN
∴AE=AN
∠6=180°-∠1-∠ABC=40°=2∠8
∴∠8=20°=∠1,
在△ABE和△FBE中,
,
∴△ABE≌△FBE(AAS),
∴AB=BF=BM+MF=BM+EM,
∴AB+AN=BM+EM+AE=AM+BM.

∵∠BAC=40°,∠ABC=120°AM,BN分别为∠BAC,∠ABC的角平分线
∴∠1=∠2=20°;∠3=∠4=60°;∠7=∠8
∴∠5=180°-∠BAC-∠3=80°=∠AEN
∴AE=AN
∠6=180°-∠1-∠ABC=40°=2∠8
∴∠8=20°=∠1,
在△ABE和△FBE中,
|
∴△ABE≌△FBE(AAS),
∴AB=BF=BM+MF=BM+EM,
∴AB+AN=BM+EM+AE=AM+BM.
点评:本题考查了角平分线定义,全等三角形的性质和判定,三角形的内角和定理,三角形的外角性质的应用,解此题的关键是能正确作出辅助线,题目比较好,难度偏大.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
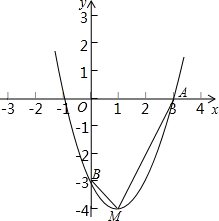 如图在直角坐标平面内,O为原点,点B坐标为(0,-3),且AO=BO,二次函数y=x2+bx+c经过A,B两点,顶点为M.
如图在直角坐标平面内,O为原点,点B坐标为(0,-3),且AO=BO,二次函数y=x2+bx+c经过A,B两点,顶点为M. 如图,有一块长为6.5单位长度,宽为2单位长度的长方形纸片,请把它分成6块,再拼成一个正方形,先在图中画出分割线,再画出拼后的图形,并标出相应的数据.
如图,有一块长为6.5单位长度,宽为2单位长度的长方形纸片,请把它分成6块,再拼成一个正方形,先在图中画出分割线,再画出拼后的图形,并标出相应的数据.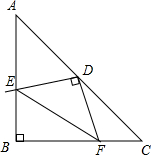 如图,在等腰△ABC中,∠ABC=90°,将直角三角板的直角顶点与AC的中点重合,把三角板绕着点D旋转,两条直角边分别交边AB于E,交边BC于F,若AB=
如图,在等腰△ABC中,∠ABC=90°,将直角三角板的直角顶点与AC的中点重合,把三角板绕着点D旋转,两条直角边分别交边AB于E,交边BC于F,若AB=