题目内容
13.将一副三角尺如图①摆放(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°).点D为AB的中点,DE交AC于点P,DF经过点C.
(1)求∠ADE的度数;
(2)如图②,在图①的基础上将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,求证:$\frac{PM}{CN}$=$\frac{PD}{CD}$.
分析 (1)首先证明∠ACD=∠A,再求出∠ADC=120°,再根据∠ADE=∠ADC-∠EDF计算即可得解;
(2)只要证明△DPM和△DCN相似,再根据相似三角形对应边成比例即可证明.
解答 解:(1)∵∠ACB=90°,点D为AB的中点,
∴CD=AD=BD=$\frac{1}{2}$AB,
∴∠ACD=∠A=30°,
∴∠ADC=180°-30°×2=120°,
∴∠ADE=∠ADC-∠EDF=120°-90°=30°;
(2)∵∠EDF=90°,
∴∠PDM+∠E′DF=∠CDN+∠E′DF=90°,
∴∠PDM=∠CDN,
∵∠B=60°,BD=CD,
∴△BCD是等边三角形,
∴∠BCD=60°,
∵∠CPD=∠A+∠ADE=30°+30°=60°,
∴∠CPD=∠BCD,
在△DPM和△DCN中,
$\left\{\begin{array}{l}{∠PDM=∠CDN}\\{∠CPD=∠BCD}\end{array}\right.$,
∴△DPM∽△DCN,
∴$\frac{PM}{CN}$=$\frac{PD}{CD}$.
点评 本题考查了旋转的性质,相似三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,属于中考常考题型.

练习册系列答案
相关题目
4.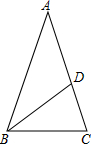 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )| A. | 30° | B. | 40° | C. | 36° | D. | 45° |
8.我国属于水资源缺乏的国家之一,节约用水,人人有责.某市为了强化公民的节水意思,合理利用水资源,采用价格调控手段达到节水的目的,该市自来水价格表如下:
注:水费按月结算
(1)若某户居民3月份用水4m3,则应缴水费12元;
(2)若某户居民4月份用水8m3,求应缴水费多少元?
(3)若某户居民8月份用水xm3(其中x大于5),求应缴水费多少元?(用含x的式子表示)
(4)若某户居民9月份用水18m3,则应缴水费多少元?
| 每月用水量 | 单价 |
| 不超过5m3 | 3元/m3 |
| 超过5m3不超过10m3的部分 | 5元/m3 |
| 超过10m3的部分 | 8元/m3 |
(1)若某户居民3月份用水4m3,则应缴水费12元;
(2)若某户居民4月份用水8m3,求应缴水费多少元?
(3)若某户居民8月份用水xm3(其中x大于5),求应缴水费多少元?(用含x的式子表示)
(4)若某户居民9月份用水18m3,则应缴水费多少元?
5. 如图所示的图形是正方体的一种平面展开图,它各面上部标有数字,则数字-2的面与它对面数字之积是( )
如图所示的图形是正方体的一种平面展开图,它各面上部标有数字,则数字-2的面与它对面数字之积是( )
 如图所示的图形是正方体的一种平面展开图,它各面上部标有数字,则数字-2的面与它对面数字之积是( )
如图所示的图形是正方体的一种平面展开图,它各面上部标有数字,则数字-2的面与它对面数字之积是( )| A. | -10 | B. | 10 | C. | -8 | D. | 8 |

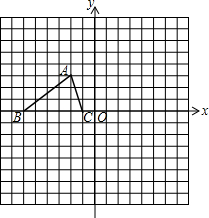 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).