题目内容
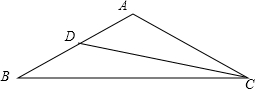
如图,等腰三角形ABC中,∠A=lOO°,CD是△ABC的角平分线,则BC写成图中两条线段的和是:BC= + .(所填线段应是图中已有字母表示的线段)

考点:等腰三角形的性质,全等三角形的判定与性质
专题:推理填空题
分析:在BC上取CE=CD,可以求出∠DEC=80°,又∠B=40°(根据等腰三角形可以求出),所以∠BDE=40°,所以BE=DE,作∠CDF=60°交BC与点F,利用SAS可以证明△ADC≌△FDC,所以AD=DF,∠DFC=∠A=100°,所以∠DFE=80°,DE=DF,从而证出BC=CD+AD.
解答:解:在边BC上截取CD=CE,连接DE.
∵等腰三角形ABC中,∠A=lOO°,
∴∠ABC=∠ACB=40°,
∵CD是∠ACB的角平分线,
∴∠ACD=∠ECD=20°,
∵CD=CE,
∴∠CDE=∠CED=80°,
∴∠BDE=∠B=40°,
∴BE=DE,
在边BC上截取CF=AC,连接DF.
∵CF=AC,∠FCD=∠ACD,CD=CD,
∴△ADC≌△FDC,
∴AD=DF,∠DFC=∠A=100°,
∴∠DFE=80°,
∴DE=DF,
∴BE=AD,
∵BC=BE+CE,
∴BC=AD+CD.
∵等腰三角形ABC中,∠A=lOO°,
∴∠ABC=∠ACB=40°,
∵CD是∠ACB的角平分线,

∴∠ACD=∠ECD=20°,
∵CD=CE,
∴∠CDE=∠CED=80°,
∴∠BDE=∠B=40°,
∴BE=DE,
在边BC上截取CF=AC,连接DF.
∵CF=AC,∠FCD=∠ACD,CD=CD,
∴△ADC≌△FDC,
∴AD=DF,∠DFC=∠A=100°,
∴∠DFE=80°,
∴DE=DF,
∴BE=AD,
∵BC=BE+CE,
∴BC=AD+CD.
点评:此题主要考查等腰三角形的性质及全等三角形的判定与性质的综合运用.

练习册系列答案
相关题目
与在数轴上表示数2的点距离等于3个单位的点所表示的数是( )
| A、-1 | B、5 |
| C、3或-3 | D、-1或5 |
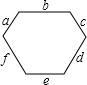 如图,一个凸六边形的六个内角都是120°,六条边的长分别为a,b,c,d,e,f,则下列等式中成立的是( )
如图,一个凸六边形的六个内角都是120°,六条边的长分别为a,b,c,d,e,f,则下列等式中成立的是( )| A、a+b+c=d+e+f |
| B、a+c+e=b+d+f |
| C、a+b=d+e |
| D、a+c=b+d |
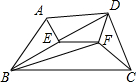 、D和这n个点为顶点作成若干个互不重叠的三角形,则所有这些三角形的内角和为
、D和这n个点为顶点作成若干个互不重叠的三角形,则所有这些三角形的内角和为