题目内容
已知|x-2|+（y+1）2=0．
（1）求x、y的值；
（2）求-x3+y4的值．
（1）求x、y的值；
（2）求-x3+y4的值．
考点：非负数的性质：偶次方,非负数的性质：绝对值
专题：
分析：（1）直接利用绝对值以及偶次方的性质得出x，y的值即可；
（2）将（1）中所求，进而求出答案．
（2）将（1）中所求，进而求出答案．
解答：解：（1）∵|x-2|+（y+1）2=0，
∴x-2=0，y+1=0，
解得：x=2，y=-1；
（2）∵x=2，y=-1，
∴-x3+y4=-23+14=-7．
∴x-2=0，y+1=0，
解得：x=2，y=-1；
（2）∵x=2，y=-1，
∴-x3+y4=-23+14=-7．
点评：此题主要考查了绝对值以及偶次方的性质，得出x，y的值是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
把抛物线y=x2+bx+c的图象向右平移3个单位，再向下平移2个单位，所得的图象的解析式是y=（x-3）2-5，则有（ ）
| A、b=3，c=0 |
| B、b=0，c=-3 |
| C、b=0，c=3 |
| D、b=3，c=-3 |
已知一元二次方程ax2+bx+c=0（a≠0）中．下列说法：①若a+b+c=0，则b2-4ac≥0；②若方程两根为-1和2，则2a+c=0；③若方程ax2+c=0有两个不相等的实根，则方程ax2+bx+c=0必有两个不相等的实根；④若b=2a+3c，则方程有两个不相等的实根．其中结论正确的有（ ）个．
| A、1个 | B、2个 | C、3个 | D、4个 |
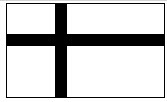如图，要设计一幅长与宽分别为30cm，20cm的图案，其中有两条彩带，横竖彩带宽度相等，如果要使彩带所占面积是图案面积的