题目内容
4. 已知一个正比例函数和一个一次函数的图象交于点P(-2,2),且一次函数图象与y轴交于点Q(0,4).
已知一个正比例函数和一个一次函数的图象交于点P(-2,2),且一次函数图象与y轴交于点Q(0,4).(1)求这两个函数的解析式;
(2)在同一坐标系中,分别画出这两个函数的图象;
(3)在x轴上找点E,使得PE+QE的值最小,并求出其最小值和点E的坐标.
分析 (1)设正比例函数解析式为y=mx,一次函数解析式为y=nx+4,将(-2,2)代入可得出两个解析式.
(2)运用两点法确定直线所在的位置.
(3)点Q关于x轴的对称点为Q′(0,-4),P、Q′连接P、Q′与x轴的交点为E,根据对称的性质可知QE=Q′E,此时PE+QE的值最小.
解答 解:(1)设正比例函数解析式为y=mx,一次函数解析式为y=nx+4,
将(-2,2)代入可得2=-2m,2=-2n+4,
解得:m=-1,n=1,
∴函数解析式为:y=-x;y=x+4.
(2)根据过点(-2.2)及(0,4)可画出一次函数图象,根据(0,0)及(-2,2)可画出正比例函数图象,如图1所示,
(3)点Q关于x轴的对称点为Q′(0,-4),
P、Q′连接P、Q′与x轴的交点为E,根据对称的性质可知QE=Q′E,此时PE+QE的值最小;
如图2,
设直线P、Q′的函数解析式为:y=kx+b,
把Q′(0,-4),P(-2,2)代入得:
$\left\{\begin{array}{l}{b=-4}\\{-2k+b=2}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-3}\\{b=-4}\end{array}\right.$,
∴y=-3x-4,
当y=0时,-3x-4=0,
解得:x=$-\frac{4}{3}$,
∴点E的坐标为(-$\frac{4}{3}$,0),
PQ′=$\sqrt{(-2-0)^{2}+(2+4)^{2}}$=2$\sqrt{10}$.
点评 本题考查待定系数法的运用,是一道综合性比较强的题目,在解答时注意抓住已知条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.4的算术平方根是( )
| A. | ±2 | B. | 2 | C. | -2 | D. | ±$\sqrt{4}$ |
19.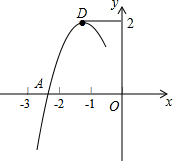 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
①b2-4ac>0;②a+b+c<0;③a=c-2;④方程ax2+bx+c=0的根为-1.
其中正确的结论为( )
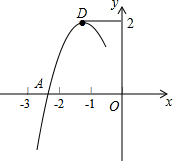 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac>0;②a+b+c<0;③a=c-2;④方程ax2+bx+c=0的根为-1.
其中正确的结论为( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
16.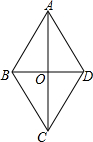 如图,已知菱形ABCD,对角线AC、BD相交于O,∠BAD=60°,则( )
如图,已知菱形ABCD,对角线AC、BD相交于O,∠BAD=60°,则( )
 如图,已知菱形ABCD,对角线AC、BD相交于O,∠BAD=60°,则( )
如图,已知菱形ABCD,对角线AC、BD相交于O,∠BAD=60°,则( )| A. | ∠ABC=60° | B. | ∠BC0=60° | C. | ∠ADO=60° | D. | ∠ADC=60° |
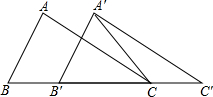 如图,在△ABC中,AB=4,BC=6,∠B=60°.将△ABC沿射线BC的方向向右平移2个单位后得到△A′B′C′,连接A′C,则△A′B′C′的面积为$6\sqrt{3}$.
如图,在△ABC中,AB=4,BC=6,∠B=60°.将△ABC沿射线BC的方向向右平移2个单位后得到△A′B′C′,连接A′C,则△A′B′C′的面积为$6\sqrt{3}$. 如图,直线y=kx+b经过A(0,-3)和B(-3,0)两点.
如图,直线y=kx+b经过A(0,-3)和B(-3,0)两点.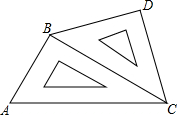 如图所示,将两个直角三角板(一个等腰直角三角形和一个含30°角的直角三角形)拼放在一起.
如图所示,将两个直角三角板(一个等腰直角三角形和一个含30°角的直角三角形)拼放在一起.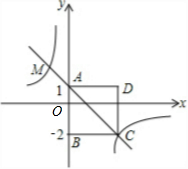 如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点
如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点