题目内容
14.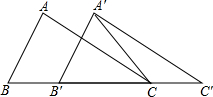 如图,在△ABC中,AB=4,BC=6,∠B=60°.将△ABC沿射线BC的方向向右平移2个单位后得到△A′B′C′,连接A′C,则△A′B′C′的面积为$6\sqrt{3}$.
如图,在△ABC中,AB=4,BC=6,∠B=60°.将△ABC沿射线BC的方向向右平移2个单位后得到△A′B′C′,连接A′C,则△A′B′C′的面积为$6\sqrt{3}$.
分析 根据平移的性质,可得答案.
解答 解:过点A作AD⊥BC,如图, ,
,
∵AD⊥BC,∠B=60°,
∴AD=$\sqrt{3}BD=\frac{\sqrt{3}}{2}AB=2\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}•BC•AD=\frac{1}{2}×6×2\sqrt{3}=6\sqrt{3}$,
∵平移不改变图形的形状和大小,
∴△A′B′C′的面积为$6\sqrt{3}$,
故答案为:$6\sqrt{3}$
点评 本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
5.下列运算正确的是( )
| A. | 4a2-2a2=2 | B. | a7÷a3=a4 | C. | 5a2•a4=5a8 | D. | (a2b3)2=a4b5 |
9.把一次函数y=-2x的图象向上平移3个单位长度,平移后,若y>0,则x的取值范围是( )
| A. | x>$\frac{3}{2}$ | B. | x<$\frac{3}{2}$ | C. | x>3 | D. | x<3 |
19. 如图,已知直线y1=x+a与y2=kx+b相交于点P(-1,2),则关于x的不等式x+a>kx+b的解集正确的是( )
如图,已知直线y1=x+a与y2=kx+b相交于点P(-1,2),则关于x的不等式x+a>kx+b的解集正确的是( )
 如图,已知直线y1=x+a与y2=kx+b相交于点P(-1,2),则关于x的不等式x+a>kx+b的解集正确的是( )
如图,已知直线y1=x+a与y2=kx+b相交于点P(-1,2),则关于x的不等式x+a>kx+b的解集正确的是( )| A. | x>1 | B. | x>-1 | C. | x<1 | D. | x<-1 |
 如图,AB=AE,AC=AD,BD=CE,△ABC≌△AED吗?试说明.
如图,AB=AE,AC=AD,BD=CE,△ABC≌△AED吗?试说明.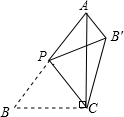 如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是1.
如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是1. 已知一个正比例函数和一个一次函数的图象交于点P(-2,2),且一次函数图象与y轴交于点Q(0,4).
已知一个正比例函数和一个一次函数的图象交于点P(-2,2),且一次函数图象与y轴交于点Q(0,4).