题目内容
某养殖户每年的养殖成本包括固定成本和可变成本，其中固定成本每年均为4万元，可变成本逐年增长，已知该养殖户第一年的可变成本为2.6万元，设可变成本平均每年增长的百分率为x．
（1）用含x的代数式表示第三年的可变成本为 万元．
（2）如果该养殖户第三年的养殖成本为7.146万元，求可变成本每年增长的百分率x，则可列方程为 ．
（1）用含x的代数式表示第三年的可变成本为
（2）如果该养殖户第三年的养殖成本为7.146万元，求可变成本每年增长的百分率x，则可列方程为
考点：由实际问题抽象出一元二次方程,列代数式
专题：
分析：（1）根据增长率问题由第1年的可变成本为2.6万元就可以表示出第二年的可变成本为2.6（1+x），则第三年的可变成本为2.6（1+x）2，故得出答案；
（2）根据养殖成本=固定成本+可变成本建立方程即可．
（2）根据养殖成本=固定成本+可变成本建立方程即可．
解答：解：（1）由题意，得
第3年的可变成本为：2.6（1+x）2，
故答案为：2.6（1+x）2；
（2）由题意，得
4+2.6（1+x）2=7.146，
故答案为：2.6（1+x）2，4+2.6（1+x）2=7.146．
第3年的可变成本为：2.6（1+x）2，
故答案为：2.6（1+x）2；
（2）由题意，得
4+2.6（1+x）2=7.146，
故答案为：2.6（1+x）2，4+2.6（1+x）2=7.146．
点评：本题考查了增长率的问题关系的运用，列一元二次方程解实际问题的运用，一元二次方程的解法的运用，解答时根据增长率问题的数量关系建立方程是关键．
练习册系列答案
阅读快车系列答案
相关题目
已知代数式x2-5x的值为6，则2x2-10x+6的值为（ ）
| A、9 | B、12 | C、18 | D、24 |
设A（-2，y1），B（1，y2），C（2，y3）是抛物线y=-（x+1）2+3上的三点，则y1，y2，y3的大小关系为（ ）
| A、y1＞y2＞y3 |
| B、y1＞y3＞y2 |
| C、y3＞y2＞y1 |
| D、y3＞y1＞y2 |
下列叙述正确的是（ ）
| A、0.4的平方根是±0.2 |
| B、±6是36的算术平方根 |
| C、-27的立方根是-3 |
| D、-（-2）3的立方根不存在 |
下列各组数中，数值相等的是（ ）
| A、32和23 |
| B、（-2）3和-23 |
| C、-32和（-3）2 |
| D、-（-2）和-|-2| |
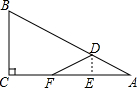如图，在△ABC中，∠C=90°，∠A=30°，BC=3，点D、E分别在AB、AC上，将△ABC沿DE折叠，点A落在AC边的点F处．若F为CE的中点，则DF的长为（ ）