题目内容
a+1+a(a+1)+a(a+1)2+…+a(a+1)2014= .
考点:因式分解-提公因式法
专题:计算题
分析:原式提取公因式,计算即可得到结果.
解答:解:原式=(a+1)[1+a+a(a+1)+a(a+1)2+…+a(a+1)2013]
=(a+1)2[1+a+a(a+1)+a(a+1)2+…+a(a+1)2012]
=(a+1)3[1+a+a(a+1)+a(a+1)2+…+a(a+1)2011]
=…
=(a+1)2015.
故答案为:(a+1)2015.
=(a+1)2[1+a+a(a+1)+a(a+1)2+…+a(a+1)2012]
=(a+1)3[1+a+a(a+1)+a(a+1)2+…+a(a+1)2011]
=…
=(a+1)2015.
故答案为:(a+1)2015.
点评:此题考查了因式分解-提公因式法,熟练掌握提取公因式的方法是解本题的关键.

练习册系列答案
相关题目
 如图,已知AD⊥CD于D,且AD=4,CD=3,AB=12,BC=13.求四边形ABCD的面积.
如图,已知AD⊥CD于D,且AD=4,CD=3,AB=12,BC=13.求四边形ABCD的面积.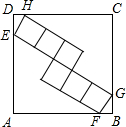 如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则每个小正方形的边长为
如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则每个小正方形的边长为