题目内容
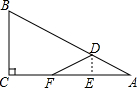如图，在△ABC中，∠C=90°，∠A=30°，BC=3，点D、E分别在AB、AC上，将△ABC沿DE折叠，点A落在AC边的点F处．若F为CE的中点，则DF的长为（ ）| A、1.5 | ||
B、
| ||
| C、2 | ||
| D、3 |
考点：翻折变换（折叠问题）
专题：
分析：首先证明CF=FE=AE，然后求出AC的长度，进而求出AE的长度问题即可解决．
解答：解：由题意得：
△ADE≌△FDE，
∴AE=FE，DF=AD，
又∵F为CE的中点，
∴CF=FE；
∴CF=FE=AE；
∵∠C=90°，∠A=30°，BC=3，
∴tan30°=
，
∴AC=
BC=3
，
∴AE=
AC=
∵cos30°=
，
∴AD=2，
∴DF=AD=2．
故该题答案为C．
△ADE≌△FDE，
∴AE=FE，DF=AD，
又∵F为CE的中点，
∴CF=FE；
∴
CF=FE=AE；∵∠C=90°，∠A=30°，BC=3，
∴tan30°=
| BC |
| AC |
∴AC=
| 3 |
| 3 |
∴AE=
| 1 |
| 3 |
| 3 |
∵cos30°=
| AE |
| AD |
∴AD=2，
∴DF=AD=2．
故该题答案为C．
点评：该命题主要考查了翻折变换及其应用问题；解题的关键是利用翻折变换的性质找出图中隐含的等量关系；借助三角形的边角关系灵活解题．
练习册系列答案
名校课堂系列答案
相关题目
若2a3x55与-4a3b2y+1是同类项，则（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
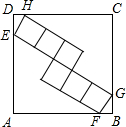如图，正方形ABCD的边长为25，内部有6个全等的正方形，小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上，则每个小正方形的边长为若（a-2）2+|b+3|=0，则（a+b）2015的值是（ ）
| A、0 | B、1 | C、-1 | D、2015 |