题目内容
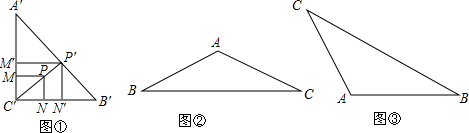
4. 如图,已知AD平分∠BAC,∠BAC+∠BDC=180°.
如图,已知AD平分∠BAC,∠BAC+∠BDC=180°.(1)若AC=CD,∠B=50°,求∠ADB;
(2)若∠C是钝角,求证:BD=CD.
分析 (1)根据四边形的内角和为360°,∠BAC+∠BDC=180°,可得∠B+∠C=180°,求出∠C的度数,利用等腰三角形的性质,求出∠DAC=∠ADC=25°,
根据AD平分∠BAC,所以∠BAC=2∠DAC=50°,得到∠BDC=130°,根据∠ADB=∠BDC-∠ADC,即可解答;
(2)过点D作DM⊥AB于M,DN⊥AC交AC延长线于N,证明△DMB≌△DNC,即可得出结论.
解答 解:(1)∵∠BAC+∠BDC=180°,
∴∠B+∠C=180°,
∵∠B=50°,
∴∠C=130°,
∵∵AC=CD,∠C=130°,
∴∠DAC=∠ADC=(180°-∠C)÷2=25°,
∵AD平分∠BAC,
∴∠BAC=2∠DAC=50°,
∵∠BAC+∠BDC=180°,
∴∠BDC=130°,
∴∠ADB=∠BDC-∠ADC=130°-25°=105°.
(2)如图,过点D作DM⊥AB于M,DN⊥AC交AC延长线于N,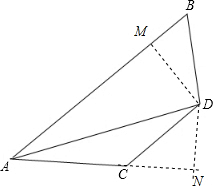
∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN,∠DMB=∠DNC=90,
∵∠ACD+∠B=180,∠ACD+∠DCN=180,
∴∠B=∠DCN,
在△BDM与△CDN中,
$\left\{\begin{array}{l}{∠B=∠DCN}\\{∠BMD=∠CND}\\{BD=DN}\end{array}\right.$,
∴△DMB≌△DNC (AAS),
∴BD=CD.
点评 本题考查了全等三角形的判定与性质,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
5.将a+b-4(a+b)合并同类项,得( )
| A. | 3a+3b | B. | -3a-3b | C. | 4b-3a | D. | 3a-3b |
16.下列各组三条线段中,不能组成三角形的是( )
| A. | a+2,a+2,a+3(a>0) | B. | 3a,5a,2a+1(a>0) | ||
| C. | 三条线段之比为1﹕2﹕3 | D. | 3cm,8cm,10cm |
13. 如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
 如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
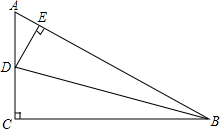 如图,D是△ACB的边AC上一点,AC⊥BC,DE⊥AB,垂足分别为点C,E,∠A=60°,DC=DE,求∠DBC的度数.
如图,D是△ACB的边AC上一点,AC⊥BC,DE⊥AB,垂足分别为点C,E,∠A=60°,DC=DE,求∠DBC的度数. 学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为627平方米,求小道的宽.
学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为627平方米,求小道的宽.