题目内容
14.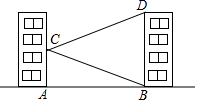 如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.(1)求∠BCD的度数.
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)
分析 (1)过点C作CE与BD垂直,根据题意确定出所求角度数即可;
(2)在直角三角形CBE中,利用锐角三角函数定义求出BE的长,在直角三角形CDE中,利用锐角三角函数定义求出DE的长,由BE+DE求出BD的长,即为教学楼的高.
解答  解:(1)过点C作CE⊥BD,则有∠DCE=18°,∠BCE=20°,
解:(1)过点C作CE⊥BD,则有∠DCE=18°,∠BCE=20°,
∴∠BCD=∠DCE+∠BCE=18°+20°=38°;
(2)由题意得:CE=AB=30m,
在Rt△CBE中,BE=CE•tan20°≈10.80m,
在Rt△CDE中,DE=CD•tan18°≈9.60m,
∴教学楼的高BD=BE+DE=10.80+9.60≈20.4m,
则教学楼的高约为20.4m.
点评 此题考查了解直角三角形的应用-仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.

练习册系列答案
相关题目
9.下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(环) | 9.14 | 9.15 | 9.14 | 9.15 |
| 方差 | 6.6 | 6.8 | 6.7 | 6.6 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
19.计算6m6÷(-2m2)3的结果为( )
| A. | -m | B. | -1 | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
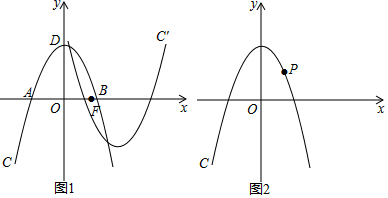
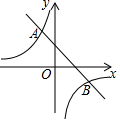 如图,一次函数y=k1x+b(k1≠0)与反比例函数y=$\frac{k_2}{x}$(k2≠0)的图象交于点A(-1,2),B(m,-1).
如图,一次函数y=k1x+b(k1≠0)与反比例函数y=$\frac{k_2}{x}$(k2≠0)的图象交于点A(-1,2),B(m,-1).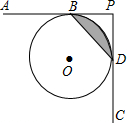 如图,直线AB,CD分别与⊙O相切于B,D两点,且AB⊥CD,垂足为P,连接BD,若BD=4,则阴影部分的面积为2π-4.
如图,直线AB,CD分别与⊙O相切于B,D两点,且AB⊥CD,垂足为P,连接BD,若BD=4,则阴影部分的面积为2π-4.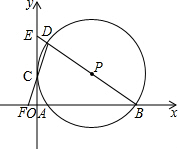 如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(-1,0),点D的坐标为(1,6).
如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(-1,0),点D的坐标为(1,6).