题目内容
20. 在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得道△BAE,连接ED,若BC=5,BD=4,则以下四个结论中:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC.其中正确的序号是( )
在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得道△BAE,连接ED,若BC=5,BD=4,则以下四个结论中:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC.其中正确的序号是( )| A. | ②③④ | B. | ①③④ | C. | ①②④ | D. | ①②③ |
分析 先由△BCD绕点B逆时针旋转60°,得到△BAE得到BD=BE,∠DBE=60°,则可判断△BDE是等边三角形;根据等边三角形的性质得BA=BC,∠ABC=∠C=∠BAC=60°,再根据旋转的性质得到∠BAE=∠BCD=60°,∠BCD=∠BAE=60°,所以∠BAE=∠ABC=60°,则根据平行线的判定方法即可得到AE∥BC;根据等边三角形的性质得∠BDE=60°,而∠BDC>60°,则可判断∠ADE≠∠BDC;由△BDE是等边三角形得到DE=BD=4,再利用△BCD绕点B逆时针旋转60°,得到△BAE,则AE=CD,所以△AED的周长=AE+AD+DE=CD+AD+DE=AC+BD.
解答 解:∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴BD=BE,∠DBE=60°,
∴△BDE是等边三角形,所以①正确;
∵△ABC为等边三角形,
∴BA=BC,∠ABC=∠C=∠BAC=60°,
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠BAE=∠BCD=60°,∠BCD=∠BAE=60°,
∴∠BAE=∠ABC,
∴AE∥BC,所以②正确;
∴∠BDE=60°,
∵∠BDC=∠BAC+∠ABD>60°,
∴∠ADE≠∠BDC,所以④错误;
∵△BDE是等边三角形,
∴DE=BD=4,
而△BCD绕点B逆时针旋转60°,得到△BAE,
∴AE=CD,
∴△AED的周长=AE+AD+DE=CD+AD+DE=AC+4=5+4=9,所以③正确.
故选D.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
19.桂林冬季里某一天最高气温是7℃,最低气温是-1℃,这一天桂林的温差是( )
| A. | -8℃ | B. | 6℃ | C. | 7℃ | D. | 8℃ |
5.分式方程$\frac{1}{x-1}$=1的解为( )
| A. | x=2 | B. | x=1 | C. | x=-1 | D. | x=-2 |
12.若一元二次方程x2+2x+m=0没有实数根,则m的取值范围是( )
| A. | m≤$\frac{1}{2}$ | B. | m>1 | C. | m≤1 | D. | m<1 |
10.已知x-$\frac{1}{x}=\frac{1}{y}$-y,且x+y≠0,则xy的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
 将△OAB绕着点O逆时针连续旋转两次得到△OA″B″,每次旋转的角度都是50°,若∠B″OA=120°,则∠AOB=20°°.
将△OAB绕着点O逆时针连续旋转两次得到△OA″B″,每次旋转的角度都是50°,若∠B″OA=120°,则∠AOB=20°°.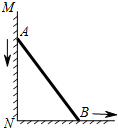 如图,一根长为5米的竹竿AB斜立于墙MN的右侧,底端B与墙角N 的距离为3米,当竹竿顶端A下滑x米时,底端B便随着向右滑行y米,反映y与x变化关系的大致图象是( )
如图,一根长为5米的竹竿AB斜立于墙MN的右侧,底端B与墙角N 的距离为3米,当竹竿顶端A下滑x米时,底端B便随着向右滑行y米,反映y与x变化关系的大致图象是( )