题目内容
8. 如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是直线x=-1.
如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是直线x=-1.(1)求抛物线对应的函数关系式;
(2)点N在线段OA上,点M在线段OB上,且OM=2ON,过点N作x轴的垂线交线段AB于点Q,交抛物线于点P.
①当ON为何值时,四边形OMPN为矩形;
②△AOQ能否为等腰三角形?若能,求出此时ON的值;若不能,请说明理由.
分析 (1)可设顶点式,根据待定系数法可求抛物线对应的函数关系式;
(2)①当四边形OMPN为矩形时,满足条件OM=PN,据此列一元二次方程求解;
②△AOQ为等腰三角形时,可能存在三种情形,需要分类讨论,逐一计算.
解答 解:(1)根据题意,设抛物线的解析式为:y=a(x+1)2+k,
∵点A(1,0),B(0,3)在抛物线上,
∴$\left\{\begin{array}{l}{4a+k=0}\\{a+k=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{k=4}\end{array}\right.$.
∴抛物线的解析式为:y=-(x+1)2+4;
(2)①设ON=t(0<t<1).
则OM=2t,PN=-(t+1)2+4,
∵四边形OMPN为矩形,
∴OM=PN,即2t=-(t+1)2+4,
整理得:t2+4t-3=0,
解得t=$\sqrt{7}$-2,由于t=-$\sqrt{7}$-2<0,故舍去,
∴当ON=$\sqrt{7}$-2时,四边形OMPN为矩形;
②Rt△AOB中,OA=1,OB=3,
∴tanA=3.
若△AOQ为等腰三角形,有三种情况: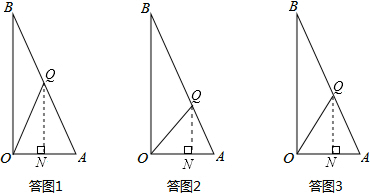
(I)若OQ=AQ,如答图1所示:
则N为OA中点,ON=$\frac{1}{2}$OA=$\frac{1}{2}$,
∴ON=$\frac{1}{2}$;
(II)若OQ=OA,如答图2所示:
设AN=x,则QD=AD•tanA=3x,ON=OA-AN=1-x,
在Rt△QON中,由勾股定理得:ON2+QN2=OQ2,
即(1-x)2+(3x)2=12,解得x1=$\frac{1}{5}$,x2=0(舍去),
∴x=$\frac{1}{5}$,ON=1-x=$\frac{4}{5}$,
∴ON=$\frac{4}{5}$;
(III)若OA=AQ,如答图3所示:
设AN=x,则QD=AN•tanA=3x,
在Rt△AQN中,由勾股定理得:QN2+AN2=AQ2,
即x2+(3x)2=12,解得x1=$\frac{{\sqrt{10}}}{10}$,x2=-$\frac{{\sqrt{10}}}{10}$(舍去),
∴ON=1-x=1-$\frac{{\sqrt{10}}}{10}$,
∴ON=1-$\frac{{\sqrt{10}}}{10}$.
综上所述,当ON为$\frac{1}{2}$、$\frac{4}{5}$、(1-$\frac{{\sqrt{10}}}{10}$)时,△AOQ为等腰三角形.
点评 本题考查了二次函数的图象与性质、待定系数法、解一元二次方程、勾股定理、解直角三角形、矩形性质、等腰三角形的性质等知识点,综合性比较强,有一定的难度.第(2)问为运动型与存在型的综合性问题,注意要弄清动点的运动过程,进行分类讨论计算.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案| A. | 了解一批袋装食品是否含有防腐剂 | |
| B. | 了解某班学生“50米跑”的成绩 | |
| C. | 了解江苏卫士“非诚勿扰”节目的收视率 | |
| D. | 调查我市冷饮市场雪糕质量情况 |
| A. | $\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=-4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-4}\\{y=-3}\end{array}\right.$ |
| A. | x2-x-1=0 | B. | x2-x+1=0 | C. | x2+x-1=0 | D. | x2-x=0 |

 如图,在△ABC中,∠BAC=90°,AB=6cm,BC=10cm,点D在线段AC上,且CD=2cm,动点P从BA的延长线上距A点10cm的E点出发,以每秒2cm的速度沿射线EA的方向运动了t秒.
如图,在△ABC中,∠BAC=90°,AB=6cm,BC=10cm,点D在线段AC上,且CD=2cm,动点P从BA的延长线上距A点10cm的E点出发,以每秒2cm的速度沿射线EA的方向运动了t秒.