题目内容
13. 如图,在平面直角坐标系中,O为坐标原点,已知点B(2,2),请在坐标轴上找一点A,使△OAB为等腰三角形,并写出所有点A的坐标.
如图,在平面直角坐标系中,O为坐标原点,已知点B(2,2),请在坐标轴上找一点A,使△OAB为等腰三角形,并写出所有点A的坐标.
分析 OB是等腰三角形的一边,确定第三点A,可以分OB是腰和底边两种情况进行讨论即可.
解答 解:(1)若BO作为腰时,有两种情况,当B是顶角顶点时,A是以B为圆心,以OB为半径的圆与坐标轴的交点,共有2个(除O点)为(0,4)(4,0);
(2)当O是顶角顶点时,A是以O为圆心,以OB为半径的圆与坐标轴的交点,有4个:(0,2$\sqrt{2}$),(0,-2$\sqrt{2}$),(2$\sqrt{2}$,0),(-2$\sqrt{2}$,0);
(3)若OB是底边时,A是OB的中垂线与坐标轴的交点,有2个:(2,0),(0,2).
以上8个交点没有重合的.
故符合条件的点A有8个:(0,4)(4,0),(0,2$\sqrt{2}$),(0,-2$\sqrt{2}$),(2$\sqrt{2}$,0),(-2$\sqrt{2}$,0),(2,0),(0,2).
点评 本题考查了坐标与图形的性质和等腰三角形的判定;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底,哪边是腰时,应在符合三角形三边关系的前提下分类讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.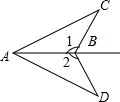 如图,已知∠1=∠2,再加上面某一条件仍无法判定△ABD≌△ABC的是( )
如图,已知∠1=∠2,再加上面某一条件仍无法判定△ABD≌△ABC的是( )
 如图,已知∠1=∠2,再加上面某一条件仍无法判定△ABD≌△ABC的是( )
如图,已知∠1=∠2,再加上面某一条件仍无法判定△ABD≌△ABC的是( )| A. | ∠CAB=∠DAB | B. | ∠C=∠D | C. | BC=BD | D. | AC=AD |
 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.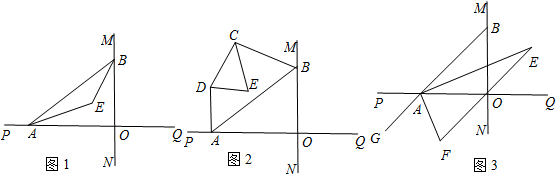
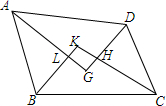 在四边形ABCD中,∠A=∠C,∠B≠∠D,则各内角平分线相交围成的四边形是梯形.
在四边形ABCD中,∠A=∠C,∠B≠∠D,则各内角平分线相交围成的四边形是梯形. 如图,在?ABCD中,∠ABC的平分线交AD于点E,且点E把AD分成5cm与4cm的两部分,求?ABCD的周长.
如图,在?ABCD中,∠ABC的平分线交AD于点E,且点E把AD分成5cm与4cm的两部分,求?ABCD的周长.