题目内容
8.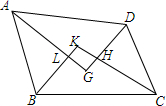 在四边形ABCD中,∠A=∠C,∠B≠∠D,则各内角平分线相交围成的四边形是梯形.
在四边形ABCD中,∠A=∠C,∠B≠∠D,则各内角平分线相交围成的四边形是梯形.
分析 根据四边形的内角和得出2∠A=360°-∠B-∠D,利用三角形内角和得出∠KLG+∠LGH=180°,进而得出LK∥GH,证明是梯形即可.
解答 解:梯形,理由如下:
∵在四边形ABCD中,∠A=∠C,∠B≠∠D,
∴2∠A=360°-∠B-∠D,
∵∠KLG=∠ALB=180°-$\frac{1}{2}∠A-\frac{1}{2}∠B$,$∠LGH=180°-\frac{1}{2}∠A-\frac{1}{2}∠D$,
∴∠KLG+∠LGH=360°-180°-$\frac{1}{2}∠B-\frac{1}{2}∠D+\frac{1}{2}∠B+\frac{1}{2}∠D$=180°,
∴LK∥GH,
∴各内角平分线相交围成的四边形是梯形.
故答案为:梯形.
点评 此题考查梯形的判定,关键是根据四边形的内角和得出2∠A=360°-∠B-∠D,利用三角形内角和得出∠KLG+∠LGH=180°.

练习册系列答案
相关题目
 如图中,由一个直角三角形和两个正方形组成,如果大正方形的面积为41,AB=5,则小正方形的面积为16.
如图中,由一个直角三角形和两个正方形组成,如果大正方形的面积为41,AB=5,则小正方形的面积为16.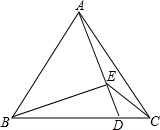 在△ABC中,AB=AC,点D在BC上,BE⊥AD于E,且∠CED=∠ACB.求证:BD=2DC.
在△ABC中,AB=AC,点D在BC上,BE⊥AD于E,且∠CED=∠ACB.求证:BD=2DC. 如图,在平面直角坐标系中,O为坐标原点,已知点B(2,2),请在坐标轴上找一点A,使△OAB为等腰三角形,并写出所有点A的坐标.
如图,在平面直角坐标系中,O为坐标原点,已知点B(2,2),请在坐标轴上找一点A,使△OAB为等腰三角形,并写出所有点A的坐标.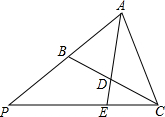 如图,在△ABC中,D为BC边上的中点,延长AD至E,使AD=2DE,连接CE并延长交AB的延长线于P,求$\frac{AB}{AP}$的值.
如图,在△ABC中,D为BC边上的中点,延长AD至E,使AD=2DE,连接CE并延长交AB的延长线于P,求$\frac{AB}{AP}$的值.