题目内容
14.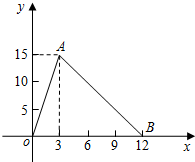 图中的折线是某类函数的图象,根据图象解答下列问题.
图中的折线是某类函数的图象,根据图象解答下列问题.(1)写出自变量x的取值范围:0≤x≤12,函数值y的取值范围:0≤y≤15;
(2)求图象能经过点A、B的一次函数的解析式.
分析 (1)根据函数图象的意义可得出x的取值范围和函数值y的范围;
(2)由图象可求得A、B两点的坐标,利用待定系数法可求得过A、B两点的直线的解析式.
解答 解:(1)由图象可知自变量x的取值范围为:0≤x≤12,
对应函数值y的取值范围为:0≤y≤15,
故答案为:0≤x≤12;0≤y≤15;
(2)由图象得A,B的坐标分别为(3,15),(12,0),
设此一次函数解析式为y=kx+b,把A、B两点坐标代入可得$\left\{\begin{array}{l}{3k+b=15}\\{12k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{5}{3}}\\{b=20}\end{array}\right.$,
∴一次函数解析式为y=-$\frac{5}{3}$x+20.
点评 本题主要考查待定系数法求函数解析式,掌握待定系数法应用的关键是点的坐标.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
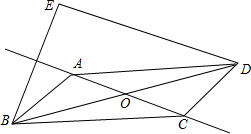 如图,在?ABCD中,对角线AC、BD相交于点O,点E为点B关于直线AC的对称点,连接EB、ED.
如图,在?ABCD中,对角线AC、BD相交于点O,点E为点B关于直线AC的对称点,连接EB、ED.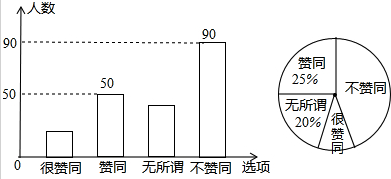
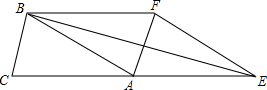 如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA的长度得到△EFA.连结BF,BE.
如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA的长度得到△EFA.连结BF,BE.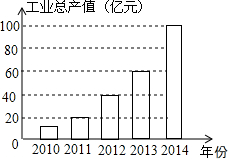 如图是根据某市2010年至2014年的工业生产总值绘制的条形统计图,观察统计图可以看出,工业生产总值(亿元)增长最多的年份是2014年.
如图是根据某市2010年至2014年的工业生产总值绘制的条形统计图,观察统计图可以看出,工业生产总值(亿元)增长最多的年份是2014年.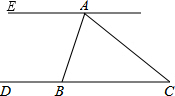 如图,在△ABC中,∠C=40°,CA=CB,过A点作EA∥BC,则∠EAB=70°.
如图,在△ABC中,∠C=40°,CA=CB,过A点作EA∥BC,则∠EAB=70°.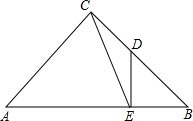 如图,△ABC是等腰三角形,∠ACB=90°,过BC的中点D作DE⊥AB,垂足为E,连接CE,求tan∠ACE的值.
如图,△ABC是等腰三角形,∠ACB=90°,过BC的中点D作DE⊥AB,垂足为E,连接CE,求tan∠ACE的值.