题目内容
如图，△ABC中，AB、BC、CA的中点分别是E，F，G，AD是高．则下列选项正确的有（ ）个（1）∠EDG=∠EFG；（2）∠B=∠BDE；（3）∠CDG=∠C；（4）∠GFC=∠ADE．
| A、1 | B、2 | C、3 | D、4 |
考点：直角三角形斜边上的中线,三角形中位线定理
专题：
分析：证明四边形AEFG是平行四边形，再根据直角三角形斜边上的中线等于斜边的一半，以及等边对等角，即可证得．
解答：解：∵AD是高，且E是AB的中点，
∴DE=BE=AE，
∴∠B=∠BDE，∠EAD=∠ADE，故（2）正确．
同理，∠DAG=∠ADG，∠CDG=∠C，则（3）正确，（4）错误；
又∵AB、BC、CA的中点分别是E，F，G，
∴EF∥AC，FG∥AE，
∴四边形AEFG是平行四边形，
∴∠EFG=∠EAG=∠EAD+∠DAG=∠ADE+∠ADG=∠EDG．故（1）正确．
故选C．
∴DE=BE=AE，
∴∠B=∠BDE，∠EAD=∠ADE，故（2）正确．
同理，∠DAG=∠ADG，∠CDG=∠C，则（3）正确，（4）错误；
又∵AB、BC、CA的中点分别是E，F，G，
∴EF∥AC，FG∥AE，
∴四边形AEFG是平行四边形，
∴∠EFG=∠EAG=∠EAD+∠DAG=∠ADE+∠ADG=∠EDG．故（1）正确．
故选C．
点评：本题考查了三角形的中位线定理以及直角三角形的性质：直角三角形斜边上的中线等于斜边的一半，和等腰三角形的性质，理解定理是关键．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
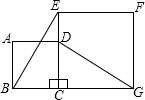如图所示，正方形ABCD的边CD在正方形ECGF的边CE上，连接BE，DG．（1）观察猜想线段BE与DG之间的大小关系，并证明你的结论；
（2）观察猜想直线BE与直线DG之间的位置关系，并证明你的结论．
如图，梯形ABCD沿上底AD方向向右平移到梯形EFGH，AD=4，BC=8，若阴影部分面积是四边形ABGH的
如图，将直线y=x沿x轴负方向平移4个单位后，恰好与双曲线y=已知sinα＜0.5，那么锐角α的取值范围是（ ）
| A、60°＜α＜90° |
| B、30°＜α＜90° |
| C、0°＜α＜60° |
| D、0°＜α＜30° |