题目内容
8.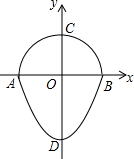 如图,是一个半圆和抛物线的一部分围成的“芒果”,已知点A、B、C、D分别是“芒果”与坐标轴的交点,AB是半圆的直径,抛物线的解析式为y=$\frac{3}{2}$x2-$\frac{3}{2}$,则图中CD的长为$\frac{5}{2}$.
如图,是一个半圆和抛物线的一部分围成的“芒果”,已知点A、B、C、D分别是“芒果”与坐标轴的交点,AB是半圆的直径,抛物线的解析式为y=$\frac{3}{2}$x2-$\frac{3}{2}$,则图中CD的长为$\frac{5}{2}$.
分析 首先令y=$\frac{3}{2}$x2-$\frac{3}{2}$=0,即可求出AB的长,进而得到OC的长,令x=0,求出y的值,进而得到OD的长,由CD=OC+DO即可求出答案.
解答 解:令y=$\frac{3}{2}$x2-$\frac{3}{2}$=0,
解得x=1或-1,
即AB=2,
故CO=1,
令x=0,解得y=-$\frac{3}{2}$,
即OD=$\frac{3}{2}$,
所以CD=CO+OD=1+$\frac{3}{2}$=$\frac{5}{2}$,
故答案为$\frac{5}{2}$.
点评 本题主要考查了抛物线与坐标轴的交点问题,理解“果圆”的定义是解题的关键,此题难度不大.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
13.电流通过导线时会产生热量,电流,(单位:A)、导线电阻R(单位:Q)、通电时间t(单位:s)与产生的热量Q(单位:J)满足Q=I2Rt.已知导线的电阻为5Ω,1s时间导线产生30J的热量,则I的值为( )
| A. | 2.4A | B. | $\sqrt{6}$A | C. | 4.8A | D. | 5$\sqrt{6}$A |
2.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表所示.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表
从上表可知,下列说法正确的个数为( )
①抛物线与x轴的一个交点为(-2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是x=$\frac{1}{2}$;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减小.
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -6 | 0 | 4 | 6 | 6 | … |
①抛物线与x轴的一个交点为(-2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是x=$\frac{1}{2}$;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减小.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,若直线y=x被双曲线y=$\frac{{k}^{2}}{x}$与双曲线y=$\frac{2{k}^{2}}{x}$在第一象限截得的线段长为2-$\sqrt{2}$.
如图,若直线y=x被双曲线y=$\frac{{k}^{2}}{x}$与双曲线y=$\frac{2{k}^{2}}{x}$在第一象限截得的线段长为2-$\sqrt{2}$.