题目内容
 如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与y轴交于点C(0,2),且与反比例函数y=
如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与y轴交于点C(0,2),且与反比例函数y=| 8 |
| x |
(1)求直线AB的函数解析式;
(2)设点P是y轴上的点,若△PBC的面积等于10,直接写出点P的坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)先由BD⊥x轴于点D,OD=2,得出点B与点D的横坐标都是2,再把x=2代入y=
,求得y=4,那么B(2,4),然后设直线AB的函数解析式为y=kx+b,将C(0,2),B(2,4)代入,利用待定系数法即可求出直线AB的函数解析式;
(2)设点P的坐标为(0,a),则PC=|a-2|.由△PBC的面积等于10,利用三角形的面积公式得出
×|a-2|×2=10,解方程求出a的值,进而得到点P的坐标.
| 8 |
| x |
(2)设点P的坐标为(0,a),则PC=|a-2|.由△PBC的面积等于10,利用三角形的面积公式得出
| 1 |
| 2 |
解答:解:(1)∵BD⊥x轴于点D,OD=2,
∴点B与点D的横坐标都是2,
把x=2代入y=
,得y=
=4,
∴B(2,4).
设直线AB的函数解析式为y=kx+b,
∵点C(0,2),B(2,4)在直线AB上,
∴
,解得
,
∴直线AB的函数解析式为y=x+2;
(2)设点P的坐标为(0,a),则PC=|a-2|.
∵△PBC的面积等于10,
∴
×|a-2|×2=10,
解得a=12或-8,
∴点P的坐标为(0,12)或(0,-8).
∴点B与点D的横坐标都是2,
把x=2代入y=
| 8 |
| x |
| 8 |
| 2 |
∴B(2,4).
设直线AB的函数解析式为y=kx+b,
∵点C(0,2),B(2,4)在直线AB上,
∴
|
|
∴直线AB的函数解析式为y=x+2;
(2)设点P的坐标为(0,a),则PC=|a-2|.
∵△PBC的面积等于10,
∴
| 1 |
| 2 |
解得a=12或-8,
∴点P的坐标为(0,12)或(0,-8).
点评:本题考查了反比例函数与一次函数的交点问题,一次函数图象上点的坐标特征,待定系数法求一次函数的解析式,三角形的面积,难度适中.求出B点的坐标是解题的关键.

练习册系列答案
相关题目
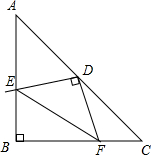 如图,在等腰△ABC中,∠ABC=90°,将直角三角板的直角顶点与AC的中点重合,把三角板绕着点D旋转,两条直角边分别交边AB于E,交边BC于F,若AB=
如图,在等腰△ABC中,∠ABC=90°,将直角三角板的直角顶点与AC的中点重合,把三角板绕着点D旋转,两条直角边分别交边AB于E,交边BC于F,若AB=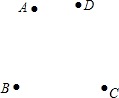 如图,学校有四幢教学楼,四幢教学楼之间是一个大操场,学校打算在操场上安置一组健身器材,使每幢教学楼的学生到健身器材处的距离和最小,请在图中画出健身器材的安置点P.
如图,学校有四幢教学楼,四幢教学楼之间是一个大操场,学校打算在操场上安置一组健身器材,使每幢教学楼的学生到健身器材处的距离和最小,请在图中画出健身器材的安置点P. 如图,线段AB=8cm.
如图,线段AB=8cm.
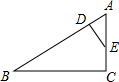 如图所示,在△ABC中,点D、E分别是△ABC的边AB、AC上的点,且AD=3,AE=6,DE=5,BD=15,CE=3,BC=15,根据以上条件,你认为∠B=∠AED吗?
如图所示,在△ABC中,点D、E分别是△ABC的边AB、AC上的点,且AD=3,AE=6,DE=5,BD=15,CE=3,BC=15,根据以上条件,你认为∠B=∠AED吗?