题目内容
11.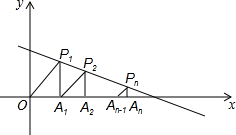 如图所示,在函数y=-$\frac{1}{3}$x+$\frac{4}{3}$(x>0)的图象上,△P1OA,△P2A1A2,△P2A2A3,…,△PnAn-1An都是等腰直角三角形,且直角边OA1,A1A2,…,An-1An都在x轴上,则An的坐标为Pn[1+$\frac{3}{4}$+$\frac{9}{16}$+…($\frac{3}{4}$)n-1,($\frac{3}{4}$)n-1].
如图所示,在函数y=-$\frac{1}{3}$x+$\frac{4}{3}$(x>0)的图象上,△P1OA,△P2A1A2,△P2A2A3,…,△PnAn-1An都是等腰直角三角形,且直角边OA1,A1A2,…,An-1An都在x轴上,则An的坐标为Pn[1+$\frac{3}{4}$+$\frac{9}{16}$+…($\frac{3}{4}$)n-1,($\frac{3}{4}$)n-1].
分析 依次设△P1OA,△P2A1A2,△P2A2A3,…的边长为a,b,c,…,把对应点P1(a,a),P2(a+b,b),P3(a+b+c,c),…,代入函数解析式,得出对应坐标数值,找出计算规律解决问题.
解答 解:设△P1OA,△P2A1A2,△P2A2A3,…的边长为a,b,c,…,
则点P1(a,a),P2(a+b,b),P3(a+b+c,c),…,
代入函数y=-$\frac{1}{3}$x+$\frac{4}{3}$(x>0),得
a=-$\frac{1}{3}$a+$\frac{4}{3}$,a=1,点P1(1,1),
b=-$\frac{1}{3}$(1+b)+$\frac{4}{3}$,b=$\frac{3}{4}$,点P2(1+$\frac{3}{4}$,$\frac{3}{4}$),
c=-$\frac{1}{3}$(1+$\frac{3}{4}$+c)+$\frac{4}{3}$,c=$\frac{9}{16}$,点P3(1+$\frac{3}{4}$+$\frac{9}{16}$,$\frac{9}{16}$),
…
因此点Pn[1+$\frac{3}{4}$+$\frac{9}{16}$+…($\frac{3}{4}$)n-1,($\frac{3}{4}$)n-1].
故答案为:Pn[1+$\frac{3}{4}$+$\frac{9}{16}$+…($\frac{3}{4}$)n-1,($\frac{3}{4}$)n-1].
点评 此题考查一次函数图象上点的坐标特征,等腰直角三角形的性质,利用待定系数法求得各个点的坐标,找出运算规律,解决问题.

练习册系列答案
相关题目
2.“比a的2倍小3的数”,用代数式表示为( )
| A. | 2a+3 | B. | 2a-3 | C. | 2(a+3) | D. | 2(a-3) |
 如图,在长方形ABCD中,AB=9,BC=15,以点B为圆心,BC长为半径画弧,交边AD于点E,则AE的长为12.
如图,在长方形ABCD中,AB=9,BC=15,以点B为圆心,BC长为半径画弧,交边AD于点E,则AE的长为12.
 如图,正方形ABCD的边长为1,P为BC上任意一点(含B、C两点),分别过点B、C、D作射线AP的垂线,垂足分别为E、F、G,以下判断:
如图,正方形ABCD的边长为1,P为BC上任意一点(含B、C两点),分别过点B、C、D作射线AP的垂线,垂足分别为E、F、G,以下判断: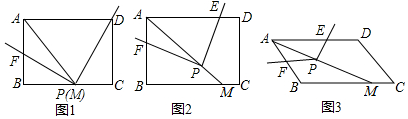
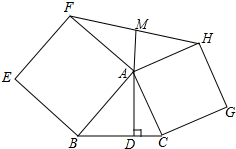 如图,分别以△ABC的边AB,AC为一边在三角形外作正方形ABEF和ACGH,M为FH上的中点,求证:MA⊥BC.
如图,分别以△ABC的边AB,AC为一边在三角形外作正方形ABEF和ACGH,M为FH上的中点,求证:MA⊥BC.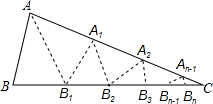 如图,△ABC中,沿∠BAC的平分线AB.折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分,…;将余下部分沿∠An-1Bn-1折叠,经过n次折叠,若点Bn-1于点C重合,就称∠ABC的n阶“完美”角.
如图,△ABC中,沿∠BAC的平分线AB.折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分,…;将余下部分沿∠An-1Bn-1折叠,经过n次折叠,若点Bn-1于点C重合,就称∠ABC的n阶“完美”角.