题目内容
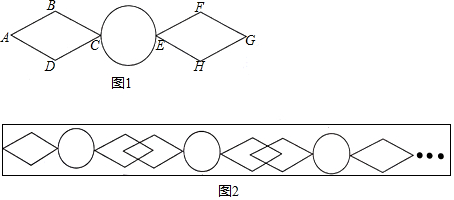
14.合肥市打造世界级国家旅游中心,精心设计12个千年古镇.如图1是某明清小院围墙中的精美图案,它是两个形状大小相同的菱形与一个圆组成,且A、C、E、G在其对称轴AG上.已知菱形的边长和圆的直径都是1dm,∠A=60°.(1)求图案中AG的长;
(2)假设小院的围墙一侧用上述图案如图2排列,其中第二块图案左边菱形一个顶点正好经过第一块图案的右边菱形的对称中心,…,依此类推,第101块这种图案这样排列长为多少米?(不考虑缝隙及拼接处)
分析 (1)连接BD,AC交于O,由于四边形ABCD是菱形,得到AC⊥BD,解直角三角形得到AO=$\frac{\sqrt{3}}{2}$,于是得到结论;
(2)根据题意得,AG=3$\sqrt{3}$+1,于是得到围墙一侧排列n块的总长2$\sqrt{3}$+1+(n-1)($\frac{\sqrt{3}}{2}$$\sqrt{3}$=1),即可得到结论.
解答  解:(1)连接BD,AC交于O,∵四边形ABCD是菱形,
解:(1)连接BD,AC交于O,∵四边形ABCD是菱形,
∴AC⊥BD,
∵AB=1,∠A=60°,
∴∠BAO=30°,
∴AO=$\frac{\sqrt{3}}{2}$,
∴AC=$\sqrt{3}$,
∵圆的直径都是1dm,
∴AG=(2$\sqrt{3}$+1)dm;
(2)根据题意得,AG=3$\sqrt{3}$+1,
而围墙一侧排列n块的总长:2$\sqrt{3}$+1+(n-1)($\frac{\sqrt{3}}{2}$$\sqrt{3}$=1),
∴第101块这种图案这样排列长为2$\sqrt{3}$+1+(101-1)($\frac{3}{2}$$\sqrt{3}$+1)=(152$\sqrt{3}$+101)dm=$\frac{152\sqrt{3}+101}{10}$米.
点评 本题考查了菱形的性质,轴对称的性质,解直角三角形,熟练掌握轴对称的性质是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
9.若3am+2b与ab2n-1是同类项,则m+n的值是( )
| A. | -1 | B. | -5 | C. | 2 | D. | 0 |
3.已知a是整数,关于q的二次三项式2q2-aq-6能在有理数范围内因式分解,则a的取值有( )种.
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
 请从以下两个小题中任选一个作答,若多选,则按第一题计分.
请从以下两个小题中任选一个作答,若多选,则按第一题计分.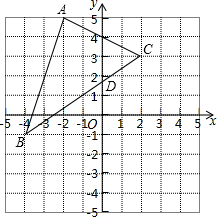 如图在平面直角坐标系中,每个小正方形的边长为一个单位长度,将△ABC向右平移3个单位长度,再向下平移4个单位长度,得到对应的△A′B′C′.
如图在平面直角坐标系中,每个小正方形的边长为一个单位长度,将△ABC向右平移3个单位长度,再向下平移4个单位长度,得到对应的△A′B′C′. 用尺规作图(不写作法,保留作图痕迹)
用尺规作图(不写作法,保留作图痕迹) 如图,四边形ABCD的对角线相交于O点,AD=BC,作AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,且DE=BF,则下列结论:
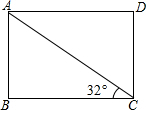
如图,四边形ABCD的对角线相交于O点,AD=BC,作AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,且DE=BF,则下列结论: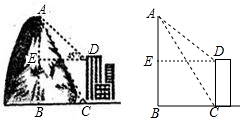 某乡镇中学教学活动小组,为测量数学楼后面的山高AB,用了如下方法.如图所示,在教学楼底C处测得山顶A的仰角为60°,在教学楼顶D处,测得山顶A的俯角为45°.已知教学楼高CD=12米,求山高AB.(结果可化为最简根式)
某乡镇中学教学活动小组,为测量数学楼后面的山高AB,用了如下方法.如图所示,在教学楼底C处测得山顶A的仰角为60°,在教学楼顶D处,测得山顶A的俯角为45°.已知教学楼高CD=12米,求山高AB.(结果可化为最简根式)