Question

10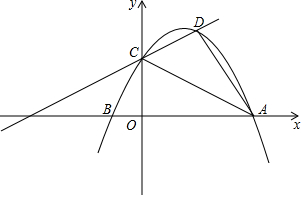．如图所示，抛物线y=ax²+bx+c的对称轴为直线x=3，与x轴的一个交点坐标为A（8，0），直线y=$\frac{1}{2}$x+4与抛物线交于y轴上的点C．
（1）求抛物线的关系式；
（2）抛物线y=ax²+bx+c与直线y=$\frac{1}{2}$x+4的另一个交点为D，连接CA、DA，求△CDA的面积．

Answer 1

分析 （1）根直线方程求得点C的坐标是（0，4），把点A、C的坐标分别代入函数关系式，以及对称轴方程联立方程组即可求得系数的值；
（2）过点D作DE垂直于x轴于点E，交AC于点F，由抛物线与直线的方程求得交点D的坐标．然后由三角形的面积公式进行解答．

解答 解：（1）∵直线y=$\frac{1}{2}$x+4与抛物线交于y轴上的点C，
∴C的坐标是（0，4），
∴$\left\{\begin{array}{l}{-\frac{b}{2a}=3}\\{0=64a+8b+c=0}\\{c=4}\end{array}\right.$
解得：$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{3}{2}}\\{c=4}\end{array}\right.$，
∴y=-$\frac{1}{4}$x²+$\frac{3}{2}$x+4；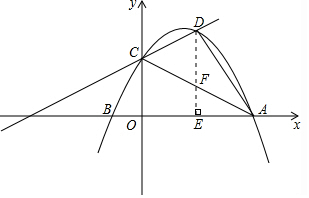

（2）过点D作DE垂直于x轴于点E，交AC于点F，
由$\left\{\begin{array}{l}{y=-\frac{1}{4}{x}^{2}+\frac{3}{2}x+4}\\{y=\frac{1}{2}x+4}\end{array}\right.$得到：$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=4}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{2}=4}\\{{y}_{2}=6}\end{array}\right.$，
则点D的坐标是（4，6）．
易求直线AC的方程为：y=-$\frac{1}{2}$x+4．
∴F（4，2），
∴S_△CDA=$\frac{1}{2}$DF•（x_A-x_C）=16．

点评 本题考查了抛物线与x轴的交点，一次函数图象上点的坐标特征以及待定系数法求二次函数解析式，解题时，注意“数形结合”数学思想的应用．