题目内容
18.如果关于x的多项式x+2与x2+mx+1的乘积中不含一次项,则m=-$\frac{1}{2}$.分析 原式利用多项式乘多项式法则计算,根据乘积中不含x的一次项,则一次项系数为0,求出m的值即可.
解答 解:(x+2)(x2+mx+1)=x3+(m+2)x2+(1+2m)x+2
∵乘积中不含一次项,
∴1+2m=0,
∴m=$-\frac{1}{2}$,
故答案为:-$\frac{1}{2}$.
点评 本题主要考查了多项式乘多项式,理解不含一次项则一次项系数为0是解本题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
3.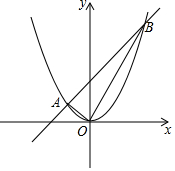 已知二次函数y=ax2的图象与一次函数y=mx+4的图象相交于点A(-2,2)和B(n,8)两点.
已知二次函数y=ax2的图象与一次函数y=mx+4的图象相交于点A(-2,2)和B(n,8)两点.
(1)求二次函数y=ax2与一次函数y=mx+4的表达式;
(2)试判断△AOB的形状,并说明理由.
 已知二次函数y=ax2的图象与一次函数y=mx+4的图象相交于点A(-2,2)和B(n,8)两点.
已知二次函数y=ax2的图象与一次函数y=mx+4的图象相交于点A(-2,2)和B(n,8)两点.(1)求二次函数y=ax2与一次函数y=mx+4的表达式;
(2)试判断△AOB的形状,并说明理由.
8.下列各式计算正确的是( )
| A. | -3+2=1 | B. | 7-(-5)=2 | C. | -2×(-0.5)=0.1 | D. | -12÷4=-3 |
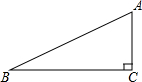 如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )



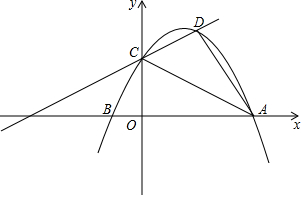 如图所示,抛物线y=ax2+bx+c的对称轴为直线x=3,与x轴的一个交点坐标为A(8,0),直线y=$\frac{1}{2}$x+4与抛物线交于y轴上的点C.
如图所示,抛物线y=ax2+bx+c的对称轴为直线x=3,与x轴的一个交点坐标为A(8,0),直线y=$\frac{1}{2}$x+4与抛物线交于y轴上的点C.