题目内容
13.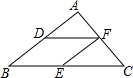 在△ABC中,AB=3,BC=4,AC=2,D、E、F分别为AB、BC、AC中点,连接DF、FE,则四边形DBEF的周长是( )
在△ABC中,AB=3,BC=4,AC=2,D、E、F分别为AB、BC、AC中点,连接DF、FE,则四边形DBEF的周长是( )| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
分析 先根据三角形中位线性质得DF=$\frac{1}{2}$BC=2,DF∥BC,EF=$\frac{1}{2}$AB=$\frac{3}{2}$,EF∥AB,则可判断四边形DBEF为平行四边形,然后计算平行四边形的周长即可.
解答 解:∵D、E、F分别为AB、BC、AC中点,
∴DF=$\frac{1}{2}$BC=2,DF∥BC,EF=$\frac{1}{2}$AB=$\frac{3}{2}$,EF∥AB,
∴四边形DBEF为平行四边形,
∴四边形DBEF的周长=2(DF+EF)=2×(2+$\frac{3}{2}$)=7.
故选B.
点评 本题考查了三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知不等式组$\left\{\begin{array}{l}{x>a}\\{x≥1}\end{array}\right.$的解集是x≥1,则a的取值范围是( )
| A. | a<1 | B. | a≤1 | C. | a≥1 | D. | a>1 |
5.下列运算正确的是( )
| A. | 2a+3b=5ab | B. | 2(2a-b)=4a-2b | C. | (a2)3=a5 | D. | a6÷a2=a3 |
2.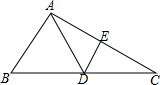 如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )
如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )
 如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )
如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )| A. | 13 | B. | 15 | C. | 17 | D. | 19 |
 甲乙都从A地出发到达B地,甲先出发0.6小时.如图所示描述两人的路程和时间的函数关系,下列说法正确的个数为( )
甲乙都从A地出发到达B地,甲先出发0.6小时.如图所示描述两人的路程和时间的函数关系,下列说法正确的个数为( )