题目内容
11.先化简,再求值:($\frac{1}{{a}^{2}-1}$+1)÷$\frac{a}{a-1}$,其中a=$\sqrt{3}$-1.分析 先将原分式化简,然后将a的值代入即可求出答案.
解答 解:当a=$\sqrt{3}$-1时,
∴原式=[$\frac{1}{(a+1)(a-1)}$+1]•$\frac{a-1}{a}$
=$\frac{1}{a(a+1)}$+$\frac{a-1}{a}$
=$\frac{1}{a(a+1)}+\frac{(a-1)(a+1)}{a(a+1)}$
=$\frac{{a}^{2}}{a(a+1)}$
=$\frac{a}{a+1}$
=$\frac{\sqrt{3}-1}{\sqrt{3}}$
=$\frac{3-\sqrt{3}}{3}$
点评 本题考查分式的化简求值,解题的关键是熟练运用分式的运算法则,本题属于基础题型

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.不等式组$\left\{\begin{array}{l}{2x+2≥0}\\{-x≥-1}\end{array}\right.$的解集在数轴上表示出来,其对应的图形为( )
| A. | 长方形 | B. | 梯形 | C. | 线段 | D. | 射线 |
6.据报道,2016年10月17日7时30分28秒,神舟十一号载人飞船在酒泉发射升空,与天宫二号在距离地面393000米的太空轨道进行交会对接,而这也是未来我国空间站运行的轨道高度393000用科学记数法表示为( )
| A. | 0.393×106 | B. | 3.93×105 | C. | 0.393×105 | D. | 39.3×104 |
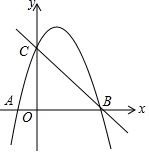 如图所示在平面直角坐标系中.抛物线y=-x2+bx+c与x轴交于A、B两点(A在B的左侧),与y轴交于C点,直线y=-x+3经过B,C 两点.
如图所示在平面直角坐标系中.抛物线y=-x2+bx+c与x轴交于A、B两点(A在B的左侧),与y轴交于C点,直线y=-x+3经过B,C 两点.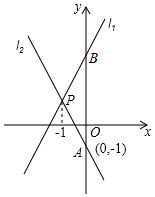 直线l1与l2相交于点P,l1的函数表达式y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).求直线l2的函数表达式及△PAB的面积.
直线l1与l2相交于点P,l1的函数表达式y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).求直线l2的函数表达式及△PAB的面积.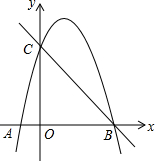 如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C
如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C